参考: https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-mamba-and-state
SSM
基础概念
状态空间(State Space)
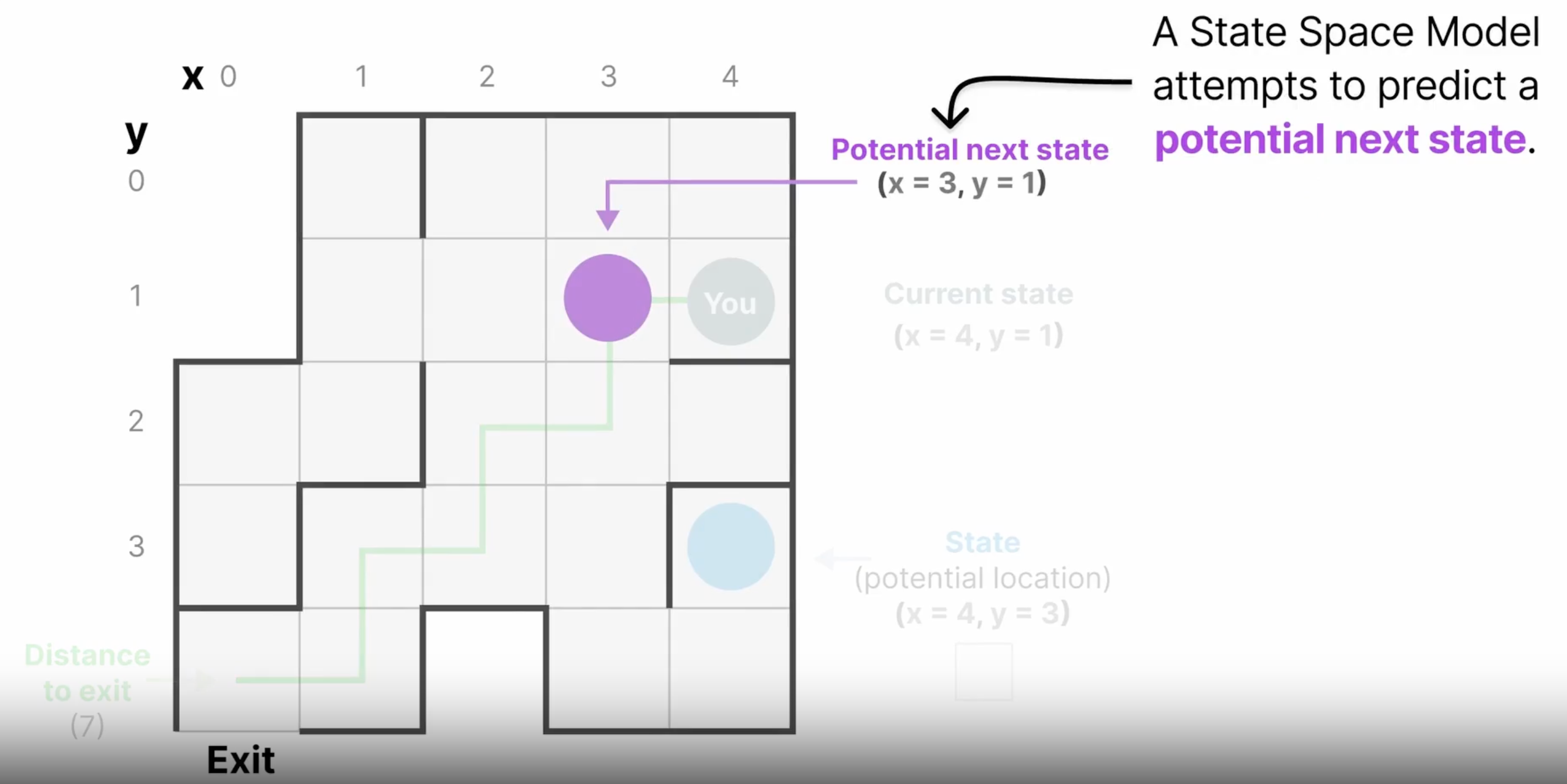
用一组变量,将系统某一时刻的信息打包,也就是状态。
举例:迷宫问题,一个状态用向量表示为(x,y,distance),即当前坐标、距离出口的距离。根据当前状态,和输入(这里是指向哪个方向走)便可预测下一个状态
为何叫 状态空间(State Space)
例子中的每个单元格都可以代表一个状态,而空间在数学上一般是封闭的,也就是说状态空间包含了所有的可能状态。
状态空间模型(State Space Model)
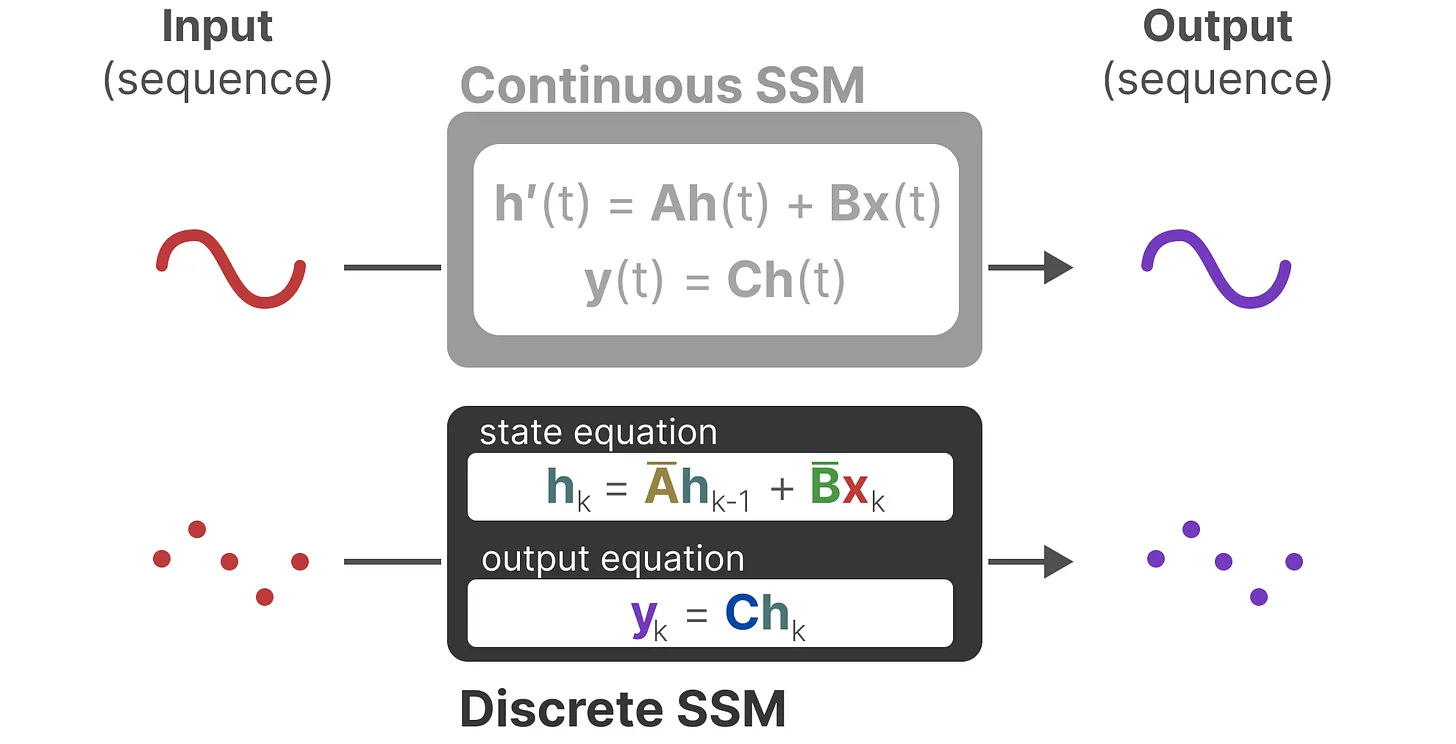
这里有连续、离散两种形式,实际上采用的是离散形式。
A,B,C,D矩阵何意味?
A,B矩阵对预测下一个状态发挥作用。
SSM中训练完成后,A,B,C,矩阵就不变了,而mamba中的相关矩阵,则是根据当前词来变化。
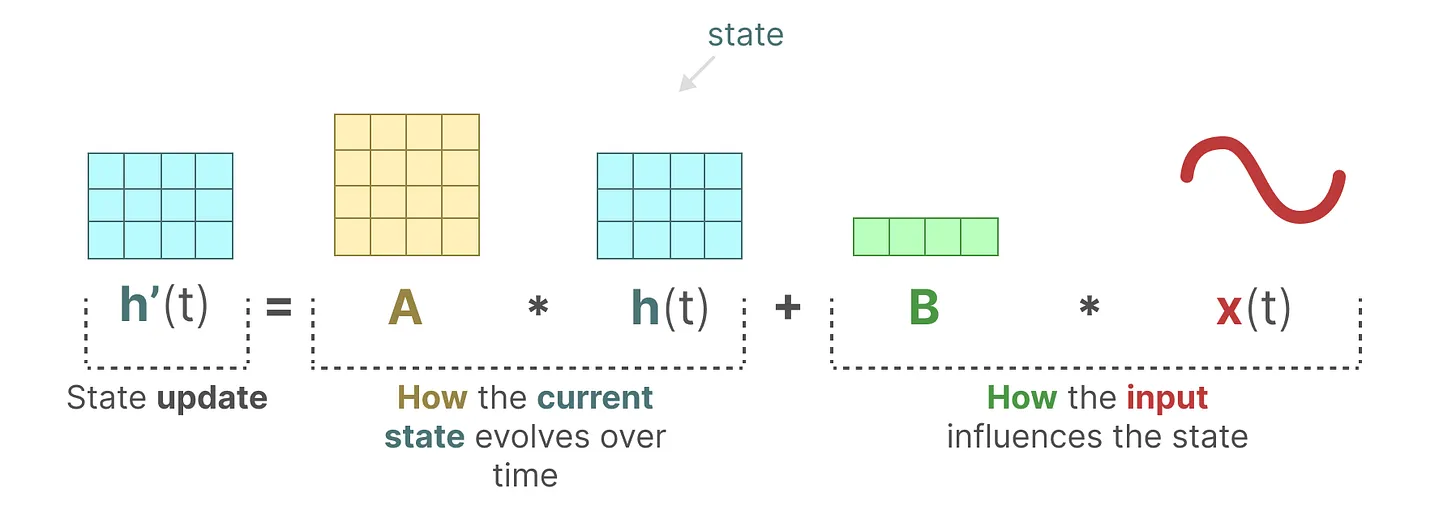
C,D对当前输出发挥作用。
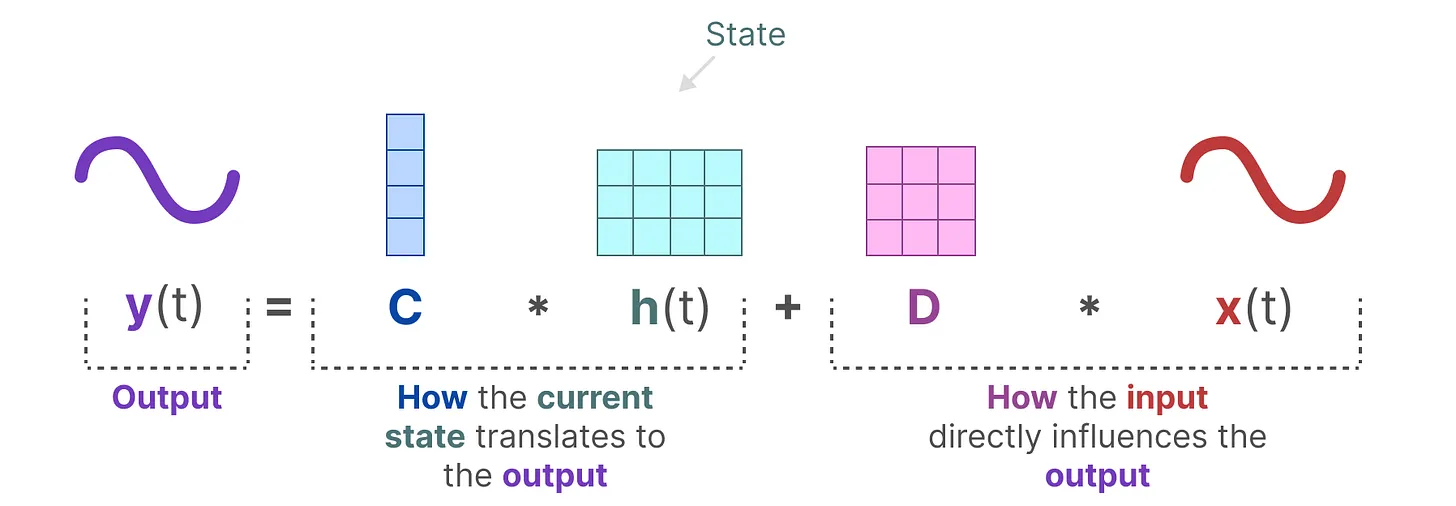
计算过程描述
输入X与B做运算,当前状态h与A做运算,相加得到下一个状态;
下一个状态同C做运算,附加上X和D矩阵的运算(这里更像是残差,帖子里用了skip-connection),得到输入y
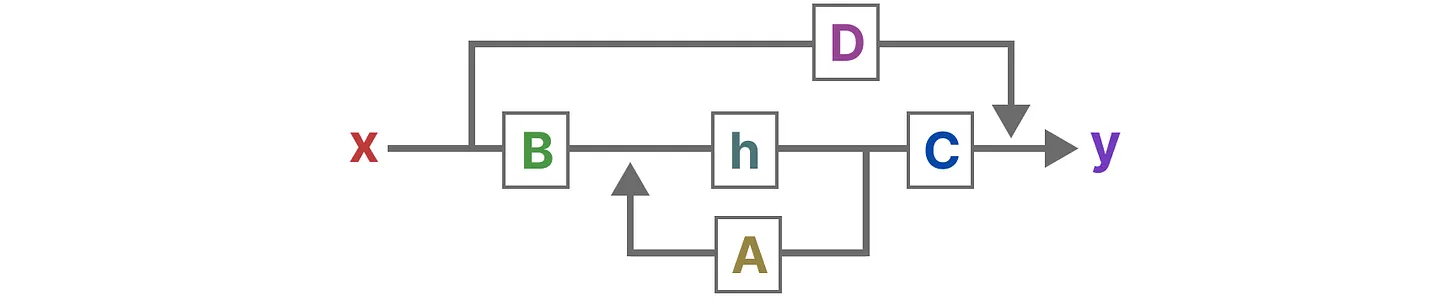
更形象的计算过程图示:
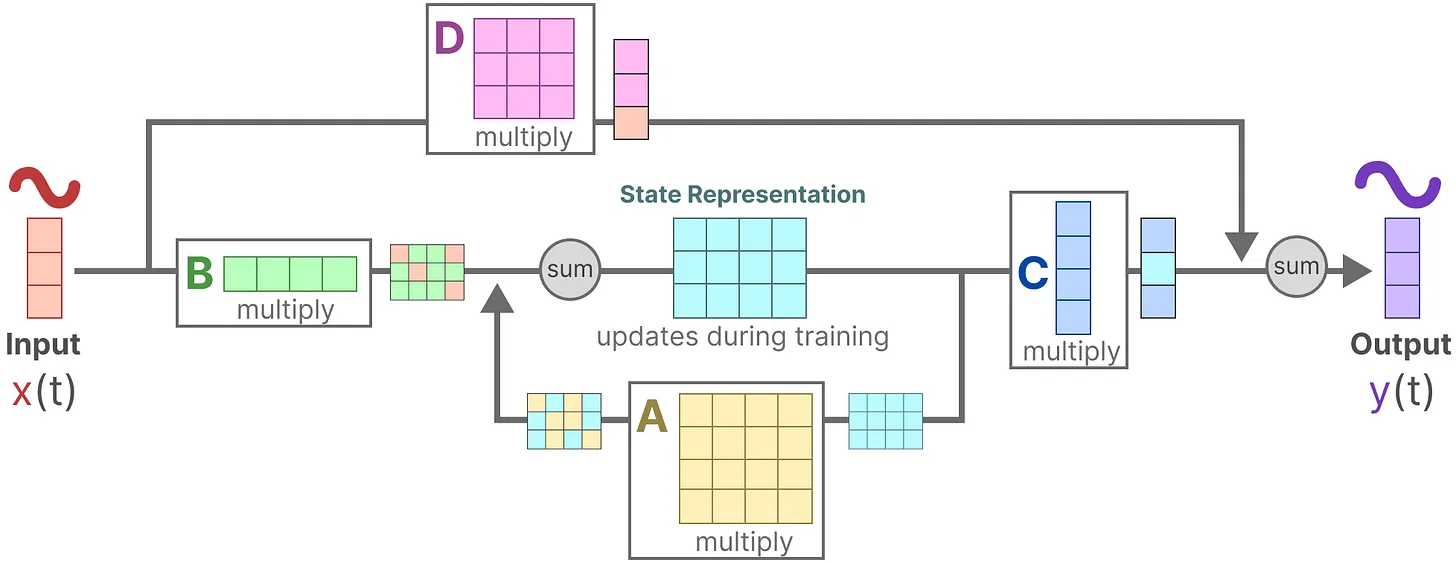
从连续到离散的转变
离散输入到连续输入,以步长$\Delta$维持一个离散输入
we make use of the Zero-order hold technique. It works as follows. First, every time we receive a discrete signal, we hold its value until we receive a new discrete signal.
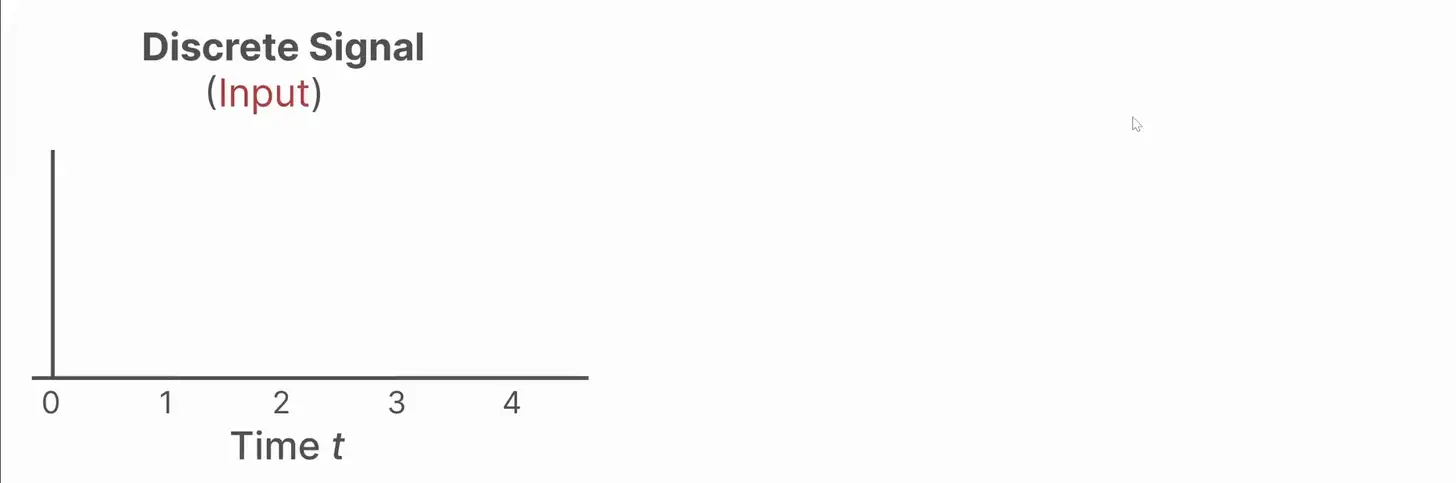
连续输入到离散输出,通过$\Delta$ 步长对连续输出进行采样
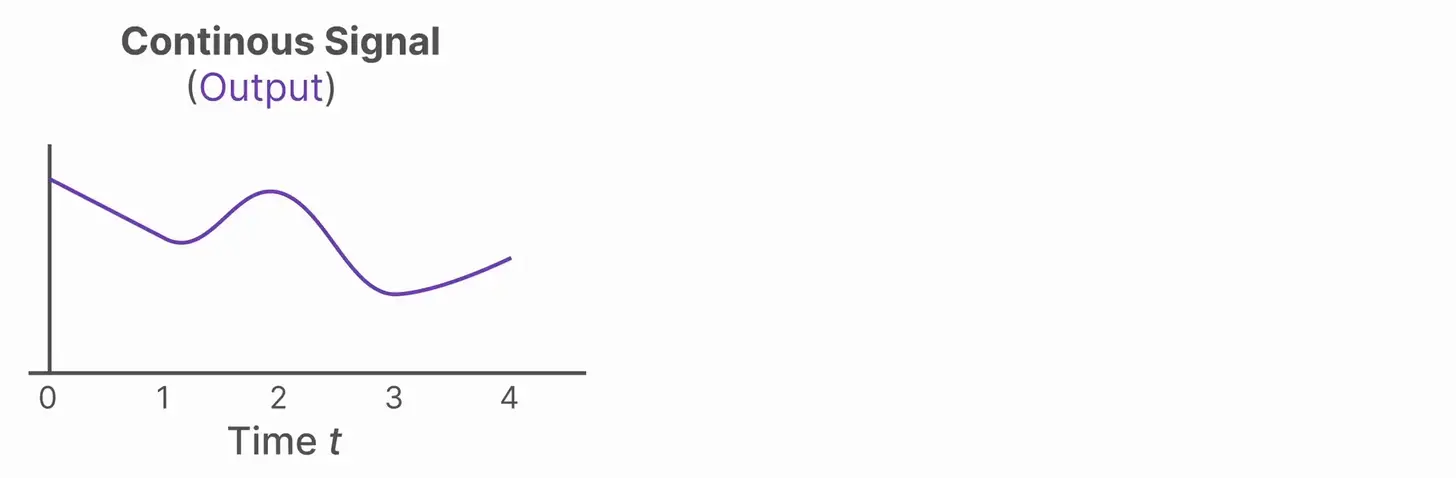
像RNN一样推理
当前的离散SSM公式
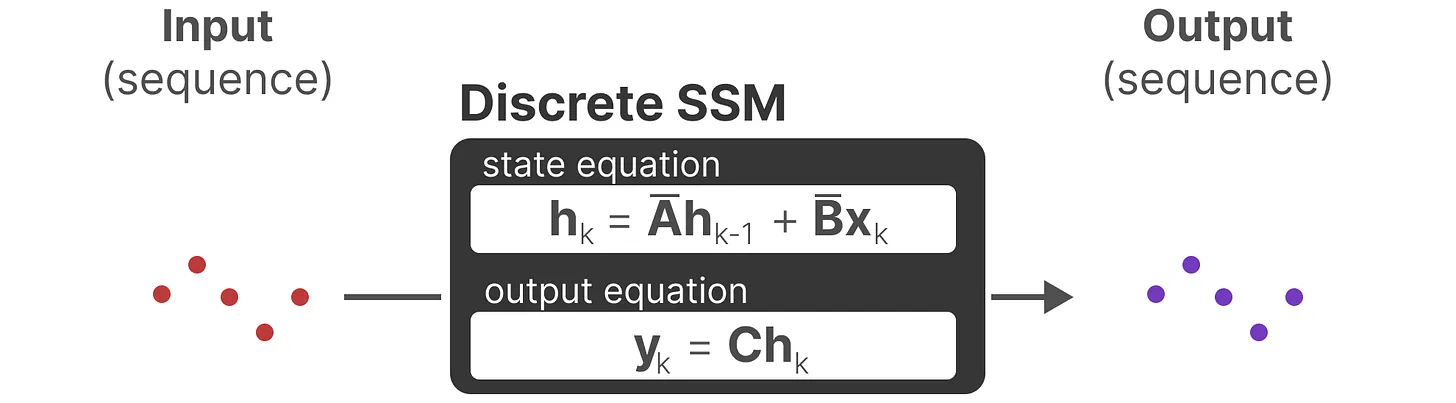
通过先前时刻状态和当前的输入,推理出当前的的状态以及输出,而不依赖于别的。
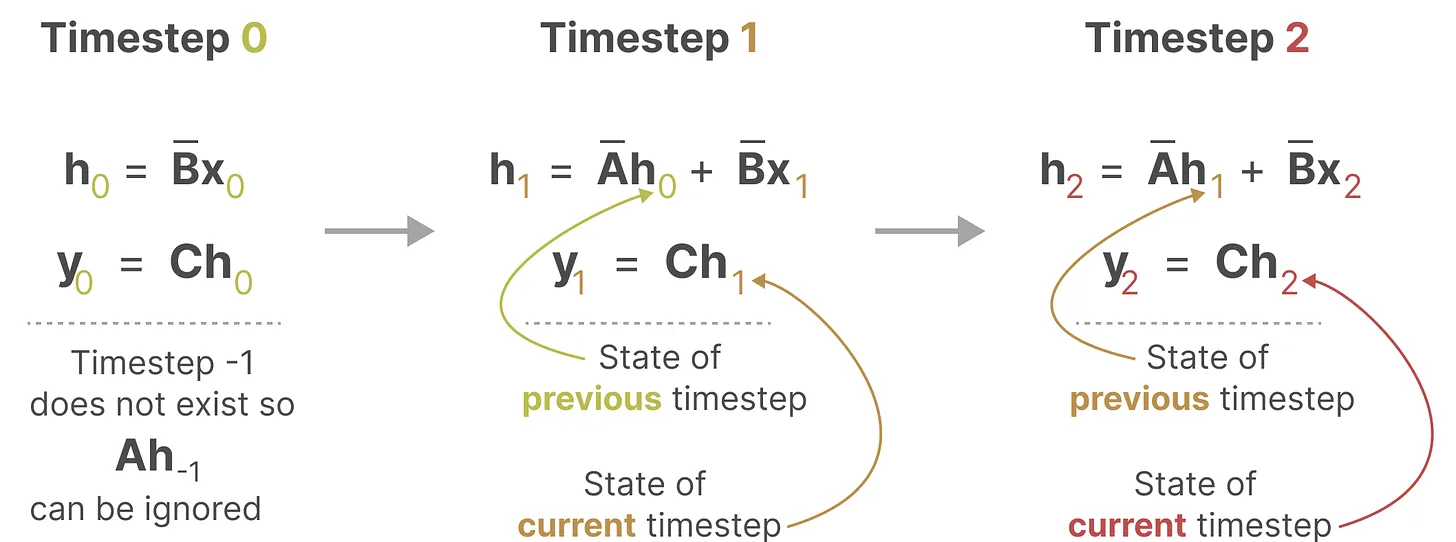
像CNN一样并行训练
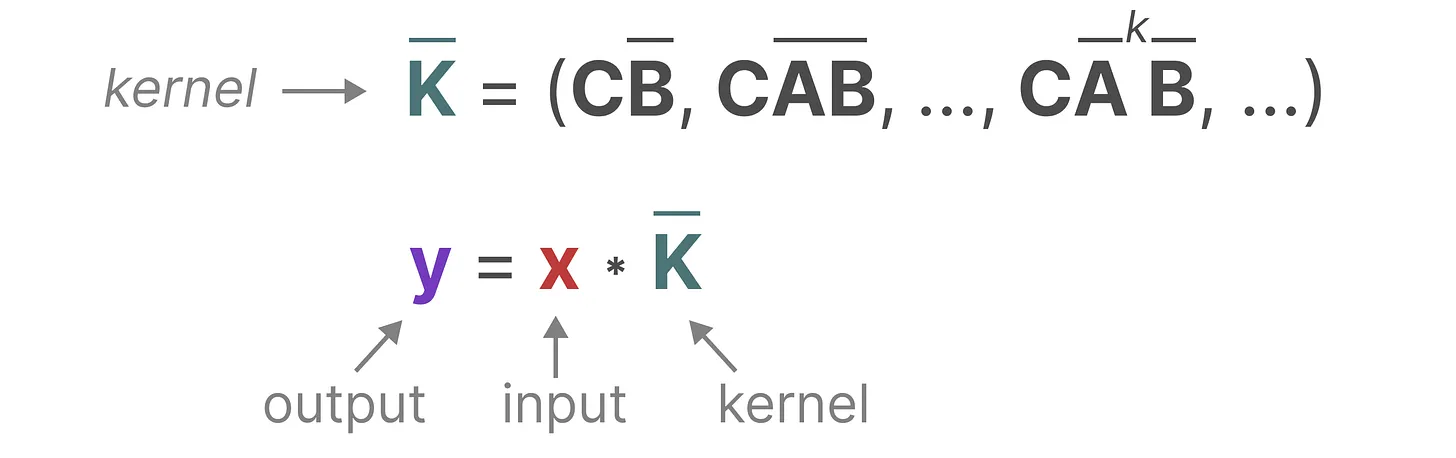
通过对公式归纳总结可以得到K,K的长度与输入长度相关
第一步:生成卷积核 K
模型根据当前的训练参数 ($\Delta, A, B, C$),通过数学变换计算出一个长度为 L(序列长度)的全局卷积核 K:
$K = (C\bar{B}, C\bar{A}\bar{B}, C\bar{A}^2\bar{B}, \dots, C\bar{A}^{L-1}\bar{B})$
注意: 这一步只需要参数,不需要看到具体的输入数据 x。
第二步:并行计算
一旦有了 K,就可以利用 FFT(快速傅里叶变换)直接计算输出:$y = x \ast K$
1维卷积核

计算过程: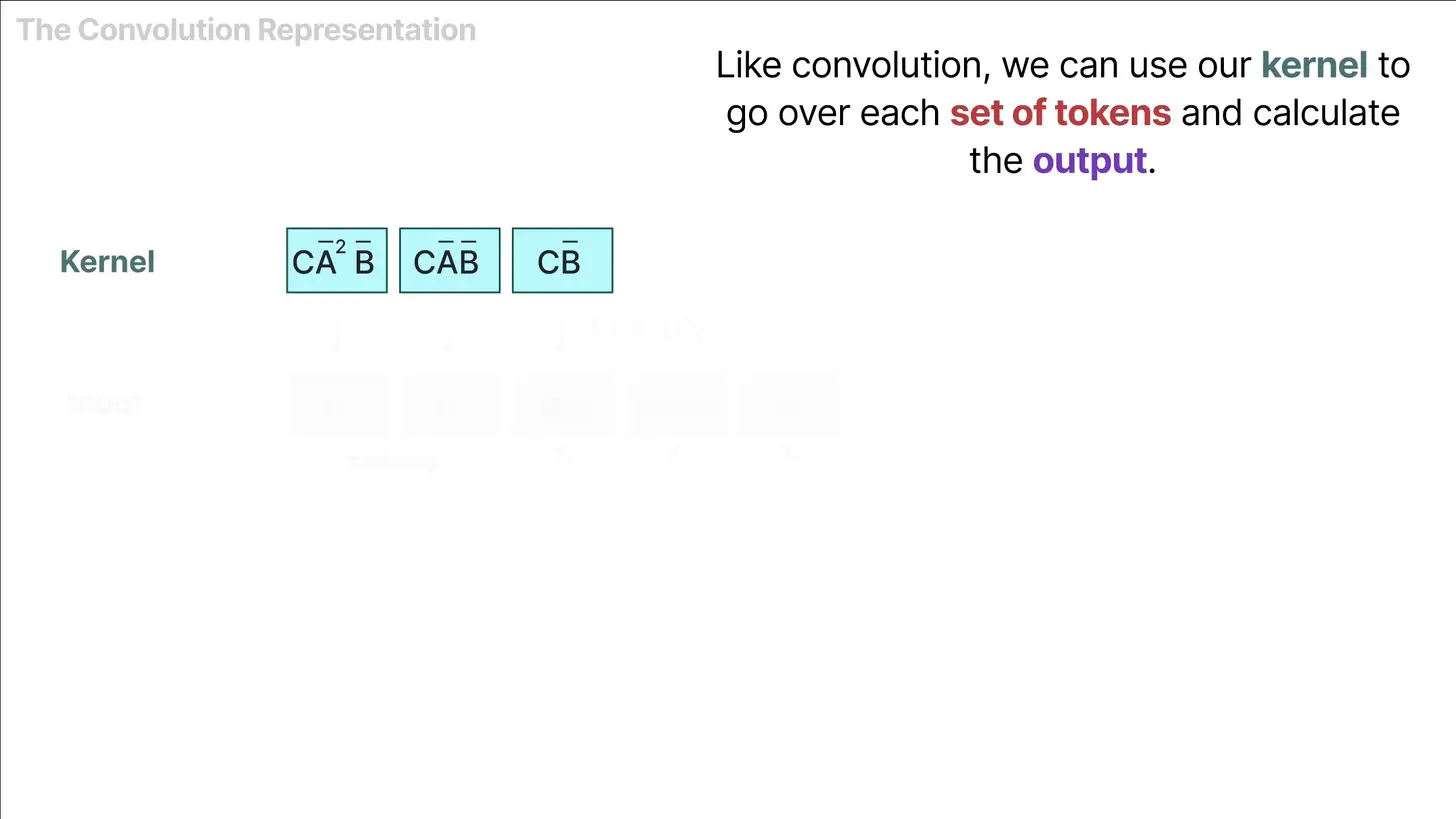
对比Mamba
“根据输入计算得到参数”**——实际上是 Mamba 的核心创新点(被称为“选择性机制”,Selection Mechanism)。
在 Mamba 中,参数 $B, C$ 和步长 $\Delta$ 不再是死板的训练参数,而是由输入 $x_t$ 动态生成的函数:
$B_t = \text{Linear}_B(x_t)$
$C_t = \text{Linear}_C(x_t)$
$\Delta_t = \text{Softplus}(\text{Parameter} + \text{Linear}_\Delta(x_t))$
后果:
因为参数随输入 $t$ 时刻而变化,它变成了时变系统,所以不能再写成一个简单的、固定的全局卷积核 $K$。
因此,Mamba 放弃了 FFT 卷积,改用 并行关联扫描(Parallel Associative Scan) 来实现训练时的并行化。
为何RNN无法并行训练?
你看我们俩多像
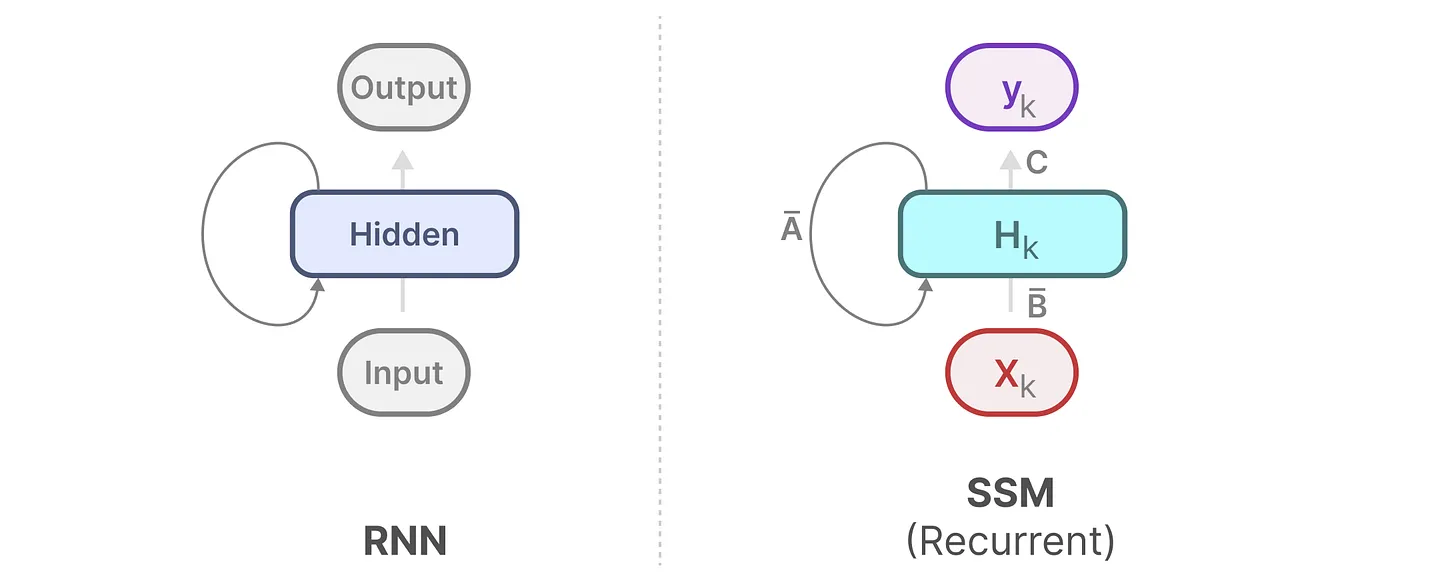
但是浮躁的公式拘缚了自由的我
RNN
隐状态更新:
$h_t = \sigma(W_{hh} h_{t-1} + W_{xh} x_t + b_h)$
输出方程:
$y_t = W_{hy} h_t + b_y$
SSM
假设当前时刻为 $t$,输入为 $x_t$,隐状态为 $h_t$,输出为 $y_t$:
状态转移方程 (State Equation):
- $h_t = \bar{A} h_{t-1} + \bar{B} x_t$
输出方程 (Output Equation):
- $y_t = C h_t + D x_t$
SSM公式是线性的,通过上述我们的推理可以得到并行的计算公式;而RNN中使用了非线性激活函数,计算顺序是固定的,也就是说必须先计算某些值,再计算另一些值。另外Linear attention中也是通过改变计算顺序,来降低计算复杂度的。
推理中与transformer的不同:
后者(transformer)预测时需要会看之前所有的词(QK计算),而前者只依赖于输入和当前状态(若从RNN或者SSM离散公式来看也可以说是上一个状态)
真正致命的瓶颈:显存带宽(Memory Bandwidth)
在现代 GPU 上,推理速度慢往往不是因为“计算(算力)”不够,而是因为**“搬运(带宽)”**太慢。这被称为 Memory-Bound(受限于显存)。
当你生成一个新词时,GPU 的核心需要做两件事:
从显存里把几十 GB 的模型参数读出来。
从显存里把已经存好的、越来越大的 KV Cache 全都读出来。
问题在于:
当你生成的文本越来越长,KV Cache 的体积会迅速膨胀。
每生成一个词,GPU 都要把整个 KV Cache 完整地从显存里“搬”到计算核心里跑一遍注意力机制。
Mamba
用于解决什么问题:transfomer对于长序列计算低效的问题。
Many subquadratic-time architectures such as linear attention,gated convolution and recurrent models, and structured state space models (SSMs) have been developed to address Transformers’ computational inefficiency on long sequences,
针对SSM的两项主要改进:
改进为输入相关(这也导致了原来的1D核并行计算失效)
新的计算方法
First, simply letting the SSM parameters be functions of the input addresses their weakness with discrete modalities, allowing the model to selectively propagate or forget information along the sequence length dimension depending on the current token. Second, even though this change prevents the use of efficient convolutions, we design a hardware-aware parallel algorithm in recurrent mode.
SSM的问题,推理时参数矩阵与输入无关
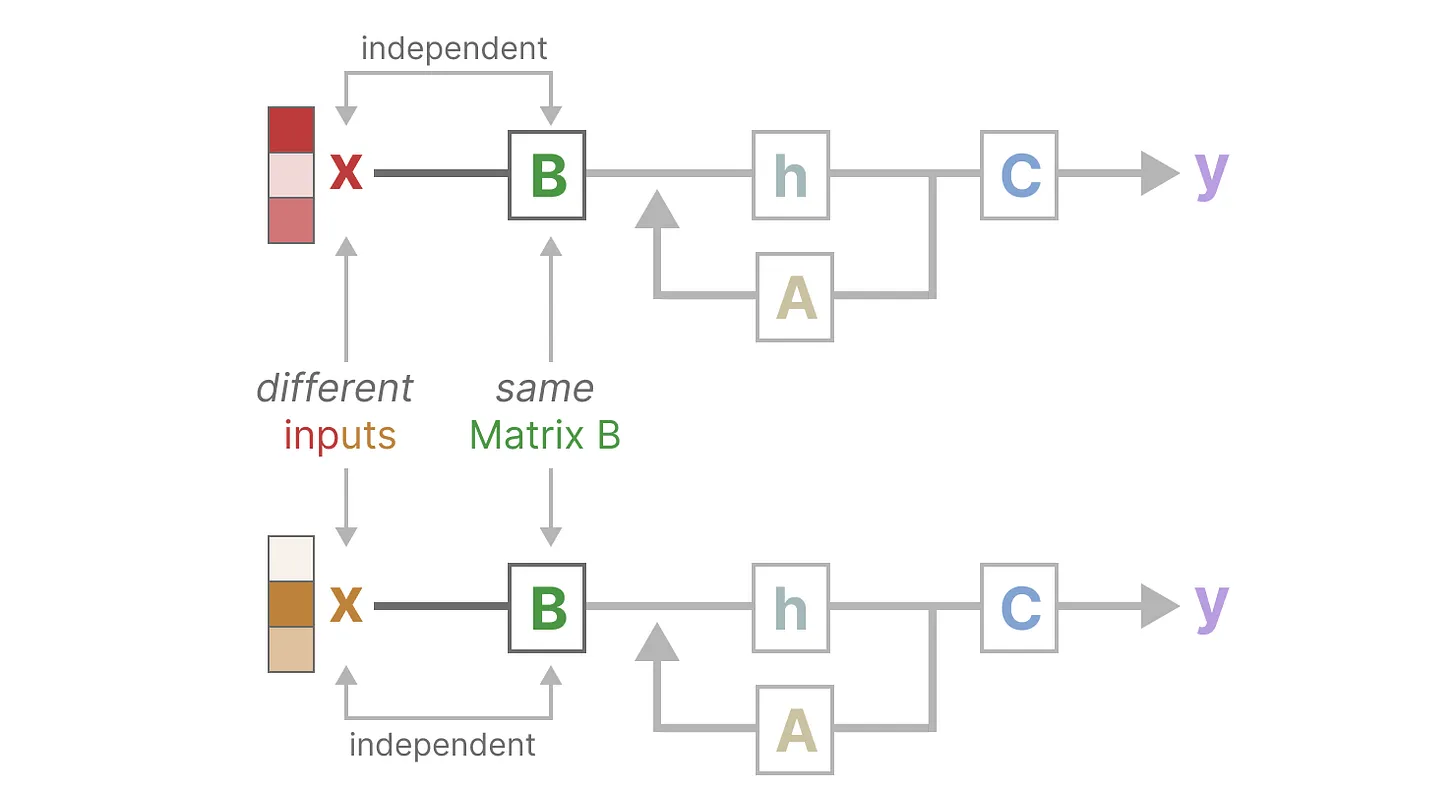
这就导致在以下两种任务中效果差
Selective Copying (选择性复制): 要求模型能够忽略序列中的大量噪声(无关 Token),只精准记住并提取特定的目标 Token。
Induction Heads (感应头): 这是 Transformer 中的一种机制。当模型看到
[A][B] ... [A]时,它能意识到当前的[A]后面应该接着出现[B]。这本质上是一种基于模式匹配的检索。
由于参数矩阵固定,与输入无关,在Selective Copying任务中难以聚焦更重要的token;
在Induction Heads任务中,更无法根据当前输入来匹配过去。
引入可变参数
参数矩阵与输入相关
Mamba makes matrices B and C, and even the step size ∆ dependent on the input by incorporating the sequence length and batch size of the input
对于每个输入都有不同的B,C矩阵
This means that for every input token, we now have different B and C matrices which solves the problem with content-awareness!
据步长 $\Delta$(Delta)来平衡“当前输入”与“历史上下文”
状态保留率(遗忘门效应):$\bar{A} = \exp(\Delta A)$
新信息摄取率(输入门效应):$\bar{B} = (\Delta A)^{-1}(\exp(\Delta A) - I) \cdot \Delta B \approx \Delta B$
当 $\Delta \to 0$ 时:
$\bar{A}$ 接近 1:由于 $\exp(0) = 1$,这意味着当前的状态 $h_t$ 几乎完美地继承了上一个状态 $h_{t-1}$。模型处于“长时间保留记忆”模式。
$\bar{B}$ 接近 0:因为 $\Delta$ 很小,新输入 $x_t$ 对状态更新的贡献微乎其微。
结论:此时模型选择忽略当前的特定单词,而是依赖于之前积累的“历史背景”。
相反$\Delta(Delta)$很大时,则聚焦当前输入。
The Scan Operation
用于训练时并行计算
为了实现训练时的并行,Scan 操作将计算拆分为两个独立部分:
第一步:预计算算子(Preprocessing)
在进行全局 Scan 之前,GPU 可以并行地计算所有的 $\bar{A}_t$ 和 $\bar{B}_t x_t$。
左侧项:计算各时间步的转移矩阵(Transition matrices)。
右侧项:计算输入项 $\bar{B}_t x_t$(即你提到的 $BX$)。
这一步是完全并行的,不涉及等待。
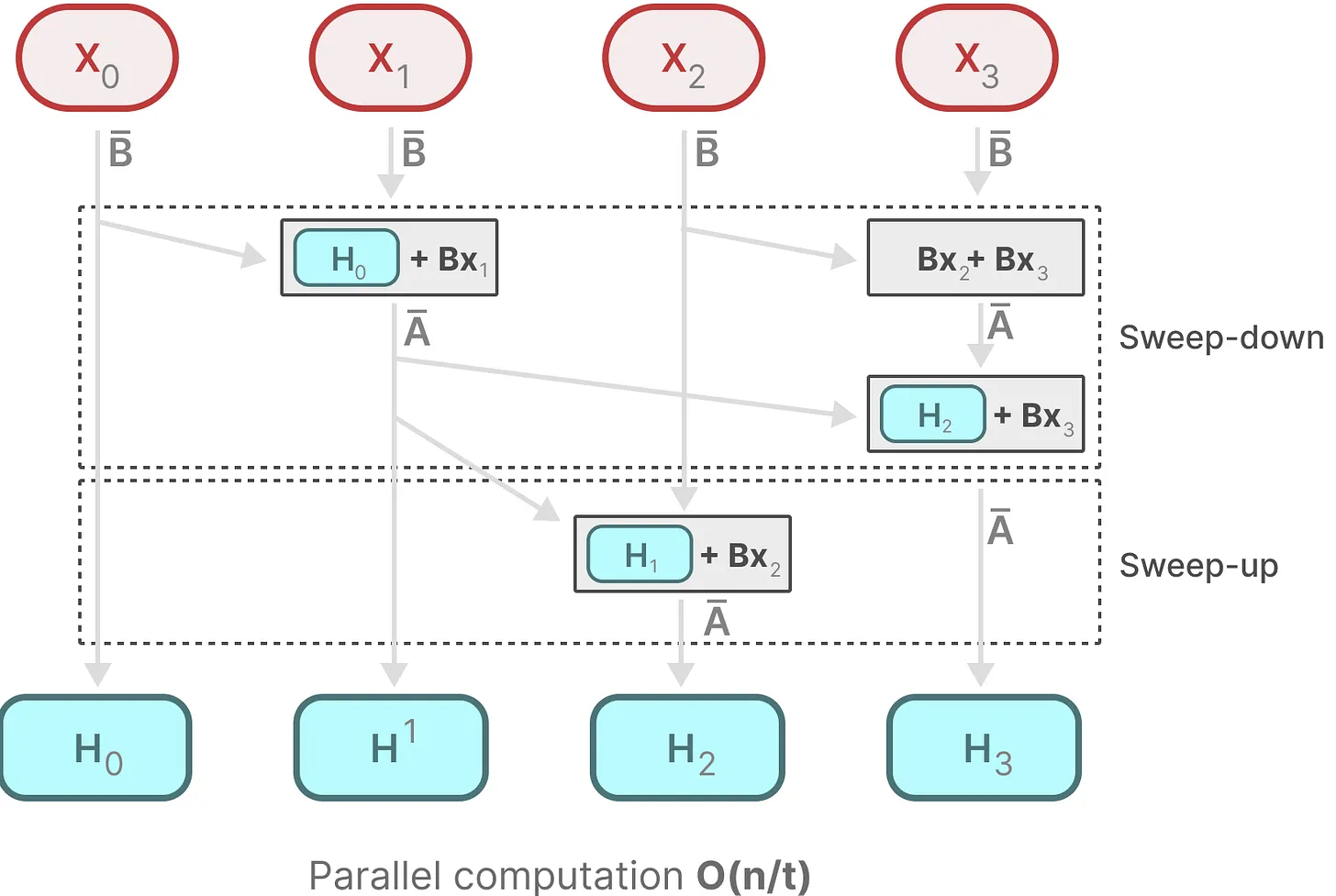
第二步:并行扫描(The Scan Operation)
利用结合律,将多个步骤合并。例如:
$h_2 = \bar{A}_2 (\bar{A}_1 h_0 + \bar{B}_1 x_1) + \bar{B}_2 x_2 = (\bar{A}_2 \bar{A}_1) h_0 + \bar{A}_2 \bar{B}_1 x_1 + \bar{B}_2 x_2$
通过这种展开,我们可以构建一个 计算树:
向上阶段(Up-sweep): 成对合并相邻的转移矩阵和输入项。
向下阶段(Down-sweep): 将合并后的结果分发下去。
这样,原本需要 $L$ 步的线性等待,变成了 $\log L$ 步的树状合并。
Hardware-aware Algorithm
用于加速计算。
由DRAM<->SRAM 间频繁的读写数据,带来的性能瓶颈;这里通过减少来回读写数据的次数,来提高性能。通过kernel fusion,不写中间结果到DRAM中,只写最终结果到DRAM中;另外反向传播中为了计算梯度,需要重新计算中间状态。