大纲:
解读顺序:由前到后,由整体到局部,由潜入深
用什么,做什么?
a recurrent neural network ,Generating coherent sketch drawings in a vector format.
怎么做?
idea:以人的思维方式进行生成,具体是模拟控笔的动作:移动方向,提笔,结束绘画
数据:$ (∆x,∆y, p1, p2, p3).$
dataset 为笔画动作,每个点由5个元素表示,分别是偏移和状态,其中偏移是相对于上一个点的偏移,状态则包含:笔尖触纸、抬笔、结束绘画
$p_1, p_2, p_3$ 是 One-hot 向量。这意味着在任意时刻,笔只能处于这三种状态中的一种(要么画,要么抬,要么停),
具体结构:
一个双向RNN编码器(Bidirectional LSTM),一个自回归的HyperLSTM解码器
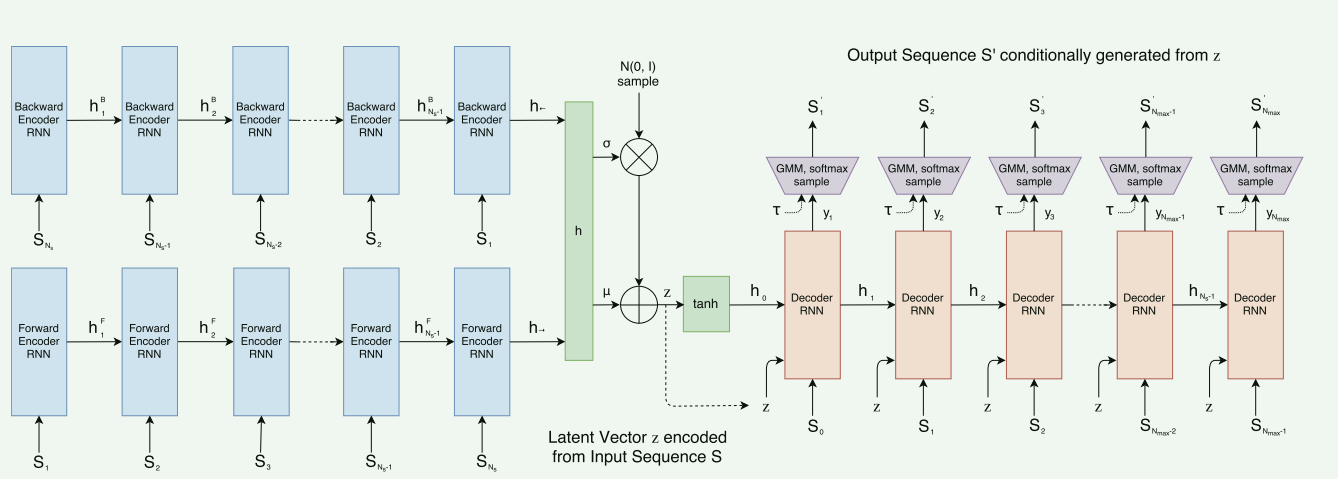
编码器:
生成h
投影到$ \mu $和 $\sigma$
得到z
- 生成h:
- 输入S到正序,反序中,输出一对h, 得到最终的h,该h便具备正向到反向的上下文信息。
$h→ = encode→(S), h← = encode←(Sreverse), h = [ h→ ; h← ]$
投影到$ \mu $和$\sigma$ 得到的h经过全连接层投影到$ \mu $和 $\sigma$ $\mu = W_{\mu}h + b_{\mu}, \quad \hat{\sigma} = W_{\sigma}h + b_{\sigma}, \quad \sigma = \exp\left(\frac{\hat{\sigma}}{2}\right)$
得到z 通过添加一定的噪声,来确定,$z = \mu + \sigma \odot \mathcal{N}(0, I)$ 为何这样做? 为了可导
对 $\mu$ 的梯度: $\frac{\partial z}{\partial \mu} = 1$
对 $\sigma$ 的梯度: $\frac{\partial z}{\partial \sigma} = \epsilon$
一个随机变量$z \sim \mathcal{N}(\mu, \sigma)$,不可导。 为何不可导?这个表达式的完整含义是:“随机变量 $z$ 将会服从一个以 $\mu$ 为中心,以 $\sigma$ 为波动范围的正态分布中随机取值。” 若分布 $\mathcal{N}(\mu+\Delta\mu, \sigma)$ 发生了轻微移动,无法确定 $z'$ 相对于 $z$ 的变化($z'$ 是新的采样结果),也就是说$z'$ 和 $\mu$ 之间缺乏确定性函数关系
过渡:z经过tanh ($[ h0 ; c0 ] = \tanh(W_z z + b_z)$)得到初始状态向量h0,c0
其中前者是初始隐藏状态,代表短期记忆,后者是初始细胞状态(LSTM 特有的),代表长期记忆(补充LSTM和RNN相关知识并实践,其中实践可以推迟)
解码器:
第一个隐藏状态 $h_0$(以及细胞状态 $c_0$)确实是通过隐向量 $z$ 投影得到的,后面的隐藏状态 $h_i$ 是通过 RNN 的前向运算(forward operation)得到的,输入是当前时间步的输入 $x_i$ 和前一时刻的状态 $[h_{i-1}; c_{i-1}]$ ,输出向量 $y_i$ 是通过将当前的隐藏状态 $h_i$ 线性投影(Fully-Connected Layer,全连接层)得到的。
$y_i = W_{y}h_{i} + b_{y}, \quad y_i \in \mathbb{R}^{6M+3} \quad \text{}$
$y_{i} = [(\hat{\Pi}_{1}\mu_{x}\mu_{y}\hat{\sigma}_{x}\hat{\sigma}_{y}\hat{\rho}_{xy})_{1} \dots (\hat{\Pi}_{1}\mu_{x}\mu_{y}\hat{\sigma}_{x}\hat{\sigma}_{y}\hat{\rho}_{xy})_{M} \quad (\hat{q}_{1}\hat{q}_{2}\hat{q}_{3})]$
我们将 $S$ 定义为相对位移向量,将 $P$ 定义为画布绝对坐标:
Step $i$ Input (输入层):
将上一时刻产生的动作向量 $S_{i-1}$ 与潜变量 $z$ 拼接。
注意:在 $i=1$(开始绘画)时,输入通常是一个特殊的“起始符”($S_0 = [0, 0, 1, 0, 0]$)。
Step $i$ Hidden (隐藏层):
$h_i = \text{LSTM}(x_i, h_{i-1}, c_{i-1})$。
这里的 $h_i$ 包含了模型对“目前画到哪了”以及“接下来该怎么画”的全部记忆。
Step $i$ Param (参数投影):
$h_i$ 通过全连接层映射到 $y_i$。
$y_i$ 包含两部分:
MDN 参数:用于决定 $\Delta x, \Delta y$ 的多个高斯分布的均值、标准差和权重。
分类参数:用于决定 $p_1, p_2, p_3$ 的概率(经过 Softmax)。
Step $i$ Sample (采样层):
从概率分布中随机采样,得到当前的动作指令 $S'_i = (\Delta x_i, \Delta y_i, p_{1,i}, p_{2,i}, p_{3,i})$。
这就是 AI 下达的“这一步怎么走”的命令。
Step $i$ Draw (渲染层):
计算终点:$P_i = P_{i-1} + (\Delta x_i, \Delta y_i)$。
执行判断:
如果 $p_{1,i} = 1$:画线连接 $P_{i-1} \to P_i$。
如果 $p_{2,i} = 1$:不画线,直接将笔尖移动到 $P_i$(提笔重定位)。
如果 $p_{3,i} = 1$:停止所有操作。
$h_i$的计算
计算 $h_i = \text{LSTM}(x_i, h_{i-1}, c_{i-1})$ 的过程可以分解为四个主要的“门控”步骤。
- 输入向量的构造
首先,输入 $x_i$ 是由两部分拼接(Concatenate)而成的:
$x_i = [S_{i-1} ; z]$
$S_{i-1}$:上一时刻的笔触向量 $(\Delta x, \Delta y, p_1, p_2, p_3)$。
$z$:来自编码器的潜变量(Latent Vector),它像是一个“总纲”,告诉解码器现在要画的是猫还是猪。
- LSTM 内部的四个“门”
LSTM 通过线性变换(权重矩阵 $W$)和激活函数($\sigma$ 或 $\tanh$)来处理 $x_i$ 和上一个隐藏状态 $h_{i-1}$。
A. 遗忘门 (Forget Gate)
决定上一时刻的记忆 $c_{i-1}$ 中有多少需要保留。
$f_i = \sigma(W_f \cdot [h_{i-1}, x_i] + b_f)$
在绘图中:如果模型发现一个线条已经画完了(比如 $S_{i-1}$ 的 $p_2=1$),遗忘门可能会“擦除”关于上一个线条方向的记忆。
B. 输入门 (Input Gate)
决定当前的新信息中有多少需要存入记忆。
$i_i = \sigma(W_i \cdot [h_{i-1}, x_i] + b_i)$
$\tilde{c}_i = \tanh(W_c \cdot [h_{i-1}, x_i] + b_c)$
$i_i$:控制保留比例。
$\tilde{c}_i$:当前时刻生成的“候选记忆”。
C. 细胞状态更新 (Cell State Update)
这是 LSTM 的核心,它更新了长期的内部状态 $c_i$。
$c_i = f_i \odot c_{i-1} + i_i \odot \tilde{c}_i$
(其中 $\odot$ 表示逐元素相乘)
D. 输出门 (Output Gate)
基于更新后的记忆,决定输出什么作为隐藏状态 $h_i$。
$o_i = \sigma(W_o \cdot [h_{i-1}, x_i] + b_o)$
$h_i = o_i \odot \tanh(c_i)$
- 计算后的去向
计算出的 $h_i$ 会立即被送往两个方向:
纵向输出:$h_i$ 进入一个全连接层,投射成 MDN(混合密度网络) 的参数。这些参数定义了 $S'_i$ 的概率分布。
横向传递:作为 $h_i$ 和 $c_i$ 传递给下一个时间步 $i+1$,成为下一次计算的输入。