基础知识补充:
期望
期望值,是指无限次重复一个随机实验,所能得到的长期平均结果。它是所有可能结果的概率加权和。
- 计算方法:每个可能的结果乘以其发生的概率,然后将所有乘积相加。
E(X)=∑[xi⋅P(X=xi)]
(对于连续型变量,使用积分)
联系By大数定律
平均值和期望值通过大数定律 被深刻地联系在一起。
大数定律指出:当试验次数(样本容量 n)足够大时,样本的平均值 xˉ 会无限接近总体的期望值 E(X)。
这就像在掷骰子的例子中,你掷的次数越多,你的平均点数就越接近理论期望值3.5。

通过例子区分平均值和期望:平均值是对已经发生的数据的概括,而期望值是对未来可能性的预测

方差
方差 是衡量随机变量与其平均值(期望值)的偏离程度的量。它描述了数据的离散程度。
计算公式:对于一个随机变量 X,其方差 Var(X) 定义为:
Var(X)=E[(X−E[X])2]直观理解:
方差大:数据点散布得很开,远离均值。不确定性高。
方差小:数据点紧密地聚集在均值周围。不确定性低。
中心极限定理
中心极限定理描述的是样本平均值分布

正态分布
正态分布描述的是数据在其平均值附近波动

正态分布的期望为 μ

区别方差和标准差
后者反应了数据在平均值上下的波动范围,前者由于是后者的平方,更多的是反映数据的分散程度,方差越大,数据越分散。
条件期望
普通期望(无条件期望):
E[y]这是随机变量
y的全局平均值。它回答的问题是:“在所有可能的情况下,y平均来看是多少?”例子:
E[身高]= 全体中国成年男性的平均身高(比如175cm)。它不考虑任何其他信息。
条件期望:
E[y | x]这是在给定某些已知信息
x的情况下,y的条件平均值。它回答的问题是:“当我们知道了某个信息x后,y平均来看是多少?”例子:
E[身高 | 年龄=10岁]= 已知一个男性年龄是10岁时,他的平均身高(比如140cm)。
核心思想:条件期望让我们能够根据已知信息,做出更精确、更“有条件”的预测。
条件期望随着条件的变化而变化:
E[房价 | 面积=50平米]= 可能是 300万(小房子更便宜)。E[房价 | 面积=200平米]= 可能是 800万(大房子更贵)。
在这里,面积 就是变量 x。条件期望 E[y | x] 是 x 的一个函数。在机器学习中,我们的模型 f(x)(比如线性回归 wᵀx)的目标,就是去近似或估计这个真实的、但通常未知的条件期望函数。
条件期望与线性回归
通常我们进行模型训练是为的到参数w来进行预测;从条件期望的视角来看,条件期望” E[y|x],在给定 x 时 y 的真实平均值,我们无法真正的得到这个平均值,但是我们模型预测是对于这个平均值的估计,其结果是近似的;而我们的训练出来的模型就是对于这样一个条件期望函数的近似。
在线性回归(乃至许多监督学习模型)中,我们并不是在预测单个的、带有噪声的数据点
y,而是在预测这些数据点的中心趋势——即条件期望E[y|x]。 我们的模型f(x)就是这个中心趋势的预测器。
线性回归的概率解释
y | x ~ N(μ, σ²),其中 μ = wᵀx
对于任何一个给定的输入
x,我预测其输出y服从一个正态分布。这个正态分布的均值μ,我通过一个线性模型wᵀx来计算得到。也就是说,y以wᵀx为中心进行随机波动。
注意一下,下面的这个链接函数,线性回归中的链接函数就等于线性预测器,要清楚这不同于逻辑回归中的链接函数
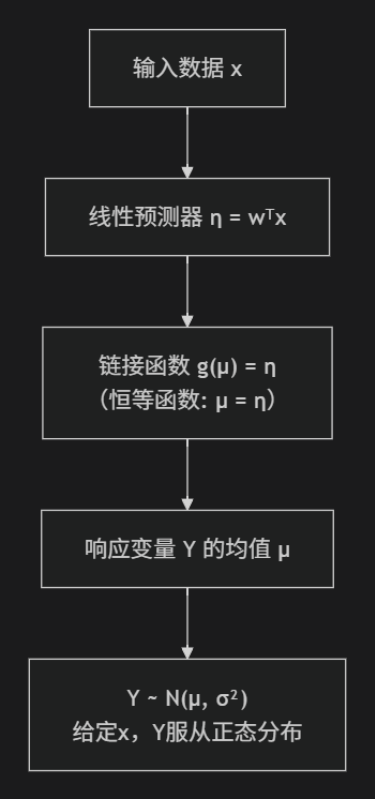
可以对比下逻辑回归的图
其中sigmod函数是通过反解logit函数得到的,最终预测结果Y服从伯努利分布
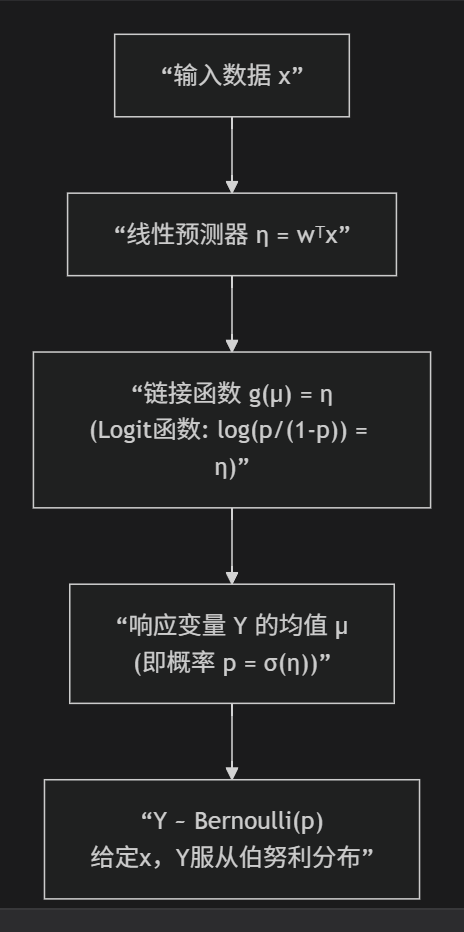
广义线性模型
线性回归:假设响应变量
y服从 高斯分布(正态分布),其均值μ通过一个恒等链接函数与线性预测器相连:μ = η = wᵀx。逻辑回归:假设响应变量
y服从 伯努利分布,其均值μ(即概率p)通过一个对数几率链接函数与线性预测器相连:log(p / (1-p)) = η = wᵀxGLM引入了一个关键概念——链接函数
g(·),它连接了线性预测器η和响应变量的均值μ:g(μ) = η
对于线性回归,链接函数是恒等函数:
μ = η对于逻辑回归,链接函数是Logit函数:
log(μ / (1-μ)) = η
泊松分布
泊松分布是一种离散概率分布,它用于描述在固定时间或空间间隔内,某个随机事件发生特定次数的概率
softmax 回归
用于处理多分类问题