标准化、归一化,用于数据预处理,一般是将原始数据统一刻度,预防原始数据差异较大带来的反向传播时的梯度爆炸。
具体刻度根据所应用的公式而不同。
Min-Max Scaling公式是,将数值归一化到[0,1]内
$x' = \frac{x - \min(x)}{\max(x) - \min(x)}$
而Z-score 公式根据实际数据将数值标准化到一定范围内
$z = \frac{x - \mu}{\sigma}$,由于每个值都减去均值,故标准化后均值为0,那为何标准化后标准差为1?实际上这种标准化在实践中也被中称为Normalization
| 特性 | 归一化 (Normalization) | 标准化 (Standardization) |
|---|---|---|
| 典型做法 | Min-Max Scaling | Z-score Normalization |
| 计算公式 | $x' = \frac{x - \min}{\max - \min}$ | $z = \frac{x - \mu}{\sigma}$ |
| 数值范围 | 严格限制在 $[0, 1]$ 或 $[-1, 1]$ | 无固定范围(通常在 $[-3, 3]$ 之间) |
| 数据中心 | 不固定 | 严格以 0 为中心 |
| 对异常值 | 非常敏感(一个极大值会把其他数压扁) | 较稳健(异常值只影响均值,不至于摧毁范围) |
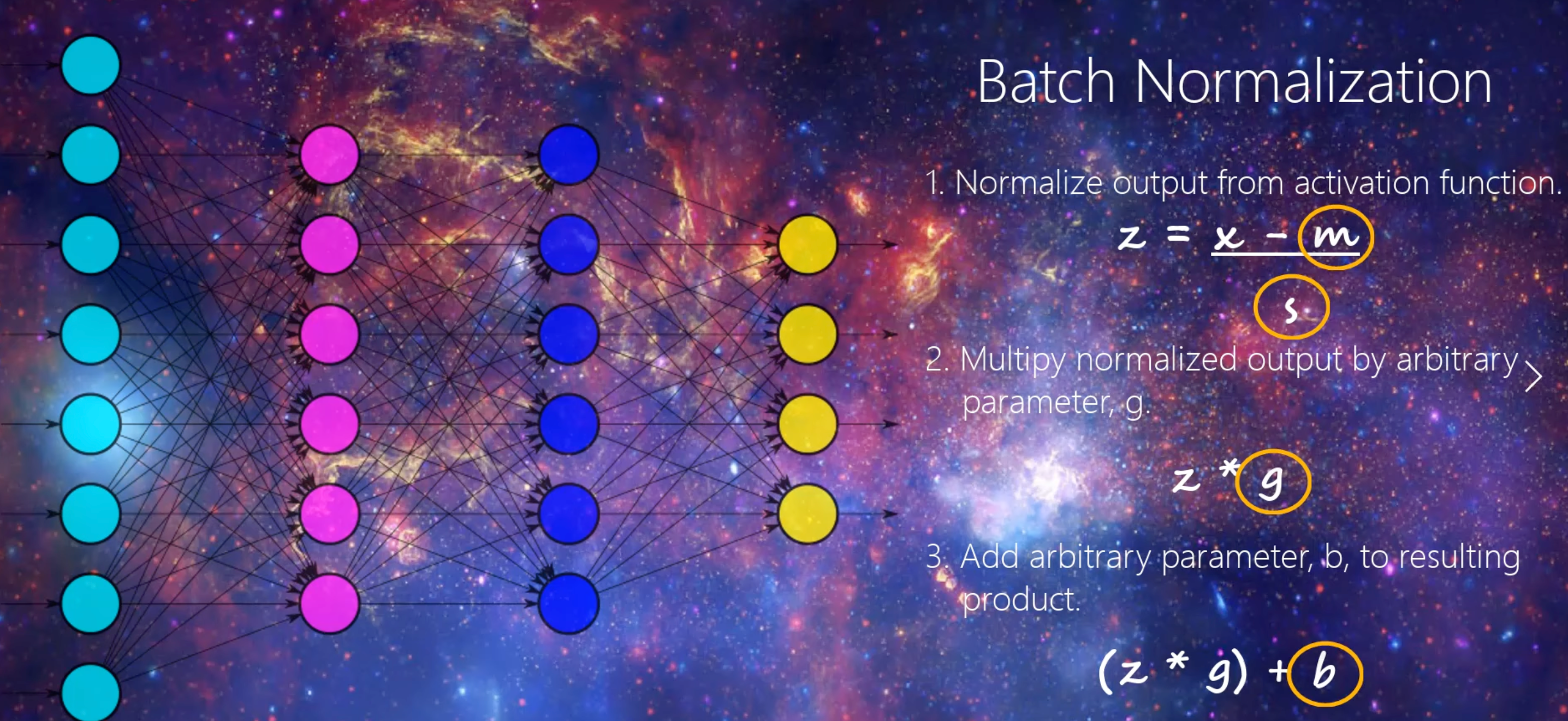
Batch Normalization
对每个Batch的神经网络输出做(特别的)Normalization,注意这里的g,b是不是标量
Batch Size = 每次神经网络输入的数据数量;epoch = 总样本量 / Batch Size