A Neural Representation of Sketch Drawings
以向量形式,生成连贯的涂鸦(低分辨率的)。
想法
以人的思维方式进行生成,具体是模拟控笔的动作:移动方向,提笔,结束绘画
什么是:unconditional and conditional generation of vector images composed of a sequence of lines.
数据
dataset 为笔画动作,每个点由5个元素表示,分别是偏移和状态,其中偏移是相对于上一个点的偏移,状态则包含:笔尖触纸、抬笔、结束绘画
方法
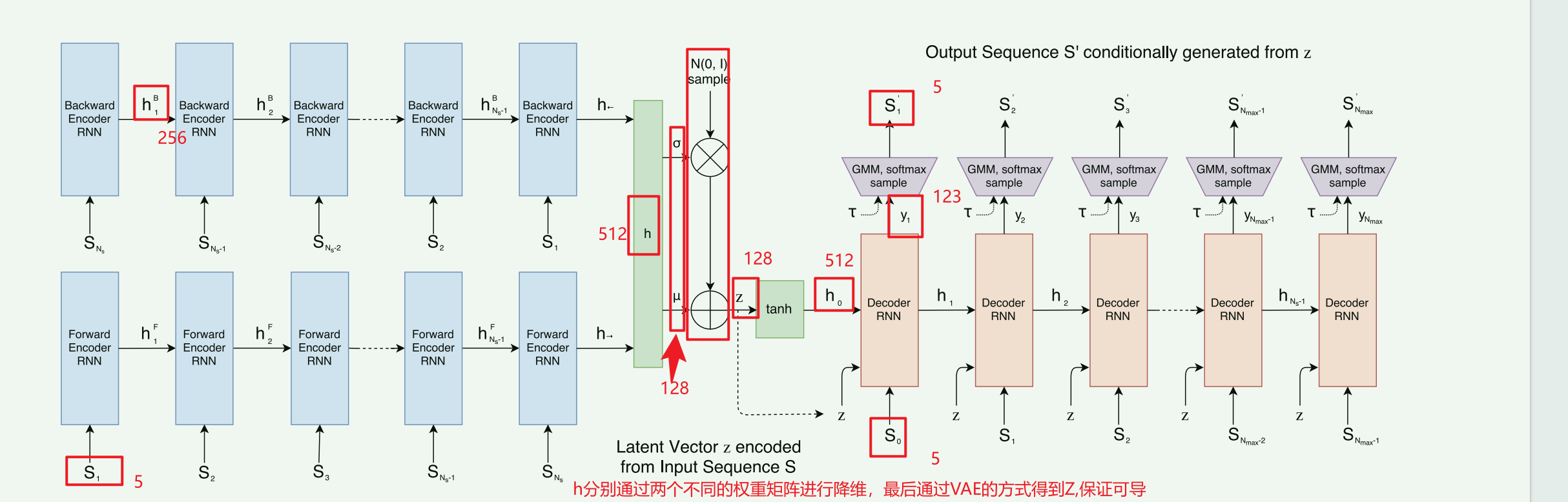
经过双向RNN 生成h,经过全连接层投影到$ \mu $和 $\sigma$,使用ex使得$\sigma$非负,再进行$z = \mu + \sigma \odot \mathcal{N}(0, I)$,其中$ \sigma \odot \mathcal{N}(0, I)$,是生成一个符合高斯分布的噪声,并使用$\sigma$进行放缩
为何这样做:
Encoder 神经网络输出 $\mu$ 和 $\sigma$ 2,实际上是在告诉系统:“我认为这张草图在潜在空间里的位置大概在这里($\mu$),但我不太确定,允许的误差范围大概是这么大($\sigma$)。
z经过tanh ($[ h0 ; c0 ] = \tanh(W_z z + b_z)$)得到初始状态向量h0,c0,其中前者是初始隐藏状态,代表短期记忆或输出状态,后者是初始细胞状态(LSTM 特有的),代表长期记忆初始细胞状态(LSTM 特有的),代表长期记忆
hi的计算方法:
根据 $h_0$(零状态)和 $S_0$ 计算出 $h_1$。
接着根据 $h_1$ 和 $S_1$ 计算出 $h_2$,以此类推
Unconditional Generation
这里是仅用解码器,那么h0初始化为0,z就没了, hi (i>0)依旧存在
生成循环 (Generation Loop)
生成过程是自回归的,每一步的输出都变成下一步的输入:
Step $i$ 的输入 ($x_i$): 在每一个时间步 $i$,输入给 RNN 的数据 $x_i$ 仅仅是前一个时间步生成的点 $S'_{i-1}$ 。
- 区别:与有条件生成不同,这里不需要拼接潜在向量 $z$ 。
Step $i$ 的输出: RNN 根据当前的内部状态和输入,计算出下一个点的概率分布参数(包括位移的高斯混合模型参数和笔触状态的分类分布参数)
采样 (Sampling): 从上述预测出的概率分布中采样得到当前的点 $S'_i$。
- 温度参数 ($\tau$):可以通过调节温度参数 $\tau$ 来控制生成的随机性。$\tau$ 越低,生成的画越确定/规范;$\tau$ 越高,生成的画越随机/混乱
重复上述循环,直到采样出的笔触状态为 $p_3=1$(结束绘画),或者达到了设定的最大序列长度 $N_{max}$ 8。
过程概述:
经过双向RNN 生成h,经过全连接层投影到$ \mu $和 $\sigma$,使用ex使得$\sigma$非负,再进行$z = \mu + \sigma \odot \mathcal{N}(0, I)$,其中$ \sigma \odot \mathcal{N}(0, I)$,是生成一个符合高斯分布的噪声,并使用$\sigma$进行放缩。z经过tanh ($[ h0 ; c0 ] = \tanh(W_z z + b_z)$)得到初始状态向量h0,c0,其中前者是初始隐藏状态,代表短期记忆或输出状态,后者是初始细胞状态(LSTM 特有的),代表长期记忆初始细胞状态(LSTM 特有的),代表长期记忆。编码器这边,z始终和si-1作为输入xi,hi(i>0)则由输入xi-1dot一个统一的权重矩阵得到,输出下一个点的分布概率yi+1,经过一系列GMM之类的处理得到一个最终的输入(此时连接了当前点和上一个点,在p1=1的情况下)
AI修正后的流程
Encode: $S \to$ Bi-RNN $\to h \to$ $(\mu, \sigma)$ $\to$ $z$。
Init: $z \to$ $[h_0; c_0]$。
Step $i$ Input: 取上一笔画完的点 $S_{i-1}$ 与 $z$ 拼接 $\to$ $x_i$。
Step $i$ Hidden: $x_i$ 进入 LSTM 单元(与 $h_{i-1}, c_{i-1}$ 交互) $\to$ $h_i$。
Step $i$ Param: $h_i$ 投影 $\to$ $y_i$ (概率参数)。
Step $i$ Sample: 从 $y_i$ 采样 $\to$ $S'_i$ (实际坐标)。
Draw: 根据 $S_{i-1}$ 的 $p_1$ 状态,决定是否画线连接 $S_{i-1}$ 和 $S'_i$
具体修正
连接动作发生在采样之后:有了 $S'_i$ 的具体数值,渲染引擎才会根据上一笔的状态 ($p_1$) 将 $S_{i-1}$ 和 $S'_i$ 连接起来。
hi的计算,LSTM 的更新过程不仅仅是一个矩阵乘法(dot),而是包含遗忘门、输入门、输出门等复杂的内部运算。$[h_i; c_i] = \text{forward}(x_i, [h_{i-1}; c_{i-1}])$ 这意味着它是通过递归调用 RNN 单元(forward operation)得到的,而不是简单的线性投影
补充
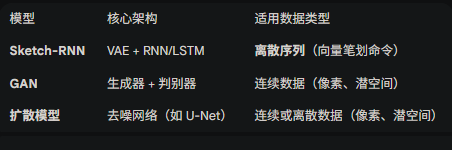
GAN 和Diffusion Models都使用 序列生成 和 潜空间 生成策略
无条件生成就是无输入随机生成,有条件生成就是给定要求下生成,其中向量图片就是矢量图。
对比GAN和Diffusion Models:
自回归模型RNN
一个模型,如果它使用自身过去(或先前)的输出作为输入,来预测未来的输出,那么它就是自回归模型
RNN之所以是自回归模型,是因为它的核心机制——隐藏状态的循环传递——决定了其在任意时间步
t的状态/输出,都依赖于它在t-1时刻的状态。这种对自身历史信息的依赖,正是自回归的本质
疑问:
why 激发p1时连接cur point to next point? 在渲染的时候如果当前点状态为p1,则读入下一个点进行连接。而在预测时是直接生成下一个点进行连接
why激发p3的点后,之后为何还有点? 为了让神经网络能够批量(Batch)处理数据,通常要求输入张量的维度是固定的,作者将所有训练数据的序列长度统一设定为 $N_{max}$,绝大多数草图的实际步数 $N_s$ 远小于 $N_{max}$为了填补 $N_s$ 到 $N_{max}$ 之间的空白,必须用数据填充。
- 填充值:论文明确指出,对于所有 $i > N_s$ 的点,将其值设定为 $(0, 0, 0, 0, 1)$ 。
所有激发p3后,仍可能有点存在。
yi的输出是什么?概率分布么? GMM用于用于生成Δx, Δy,softmax 用于判断状态 $y_i$ 的输出不是概率分布本身,而是定义概率分布所需的“参数 (Parameters 其维度大小为 $6M + 3$
$M$: 高斯混合模型中高斯分量的个数(论文中 $M=20$)
$6M$: 对应 GMM 的参数。
$3$: 对应笔触状态的 Logits。 笔触状态 Logits ($\hat{q}_1, \hat{q}_2, \hat{q}_3$): 3 个值。 处理方式: 使用 Softmax。将其转换为三个互斥状态 $(p_1, p_2, p_3)$ 的概率,且和为 1 。
为何有6个M
混合权重 ($\Pi_k$): $M$ 个值。
- 处理方式: 使用 Softmax。保证所有高斯分量的权重之和为 1 。
- 用于给M个高斯分量定权重。
均值 ($\mu_x, \mu_y$): $2M$ 个值。
- 处理方式: 直接使用(无激活函数)。因为偏移量可以是正负任意值。
标准差 ($\sigma_x, \sigma_y$): $2M$ 个值。
- 处理方式: 使用 Exp (指数函数)。保证标准差必须为正数 。
相关系数 ($\rho_{xy}$): $M$ 个值,决定了往哪个方向走
- 处理方式: 使用 Tanh。保证相关系数在 $[-1, 1]$ 之间
为何用GMM? 单个高斯分布,最大可能得预测值是均值$\mu$ ,多个高斯选项更多
单个高斯分布只有一个预测值?那么GMM中不是也只有一个预测值?这里是说GMM相比单个高斯分布,可选的更多么 单个高斯分布可选项只有平均值,而GMM可选多个均值,
1. 核心区别:敢不敢承认“分歧”
想象你的自动驾驶汽车开到了一个丁字路口,前面是墙,只能左转或右转。
情况 A:单个高斯分布(Single Gaussian)
它的逻辑:“我要预测一个最可能的方向。既然左边(-1)是对的,右边(+1)也是对的,那我取平均值吧。”
预测的分布:均值 $\mu = 0$(直直地撞向墙)。
最终采样:虽然它是一个概率分布,但概率最高的点是 0。如果你从中采样,大概率会采到 0 附近的值。
结果:撞墙。因为它把两个相反的正确答案“平均”成了一个错误的答案。
情况 B:混合高斯模型(GMM)
它的逻辑:“我知道这里有两个选择。这里有一个‘左转’的高斯分布,那里有一个‘右转’的高斯分布。中间的墙是绝对不能去的。”
预测的分布:这就不是一个预测值了,而是一张地形图。
峰值 1:在 -1 的位置(概率 50%)。
峰值 2:在 +1 的位置(概率 50%)。
谷底:在 0 的位置(概率极低)。
最终采样:
先掷骰子选一个峰(比如选了左边)。
然后在左边的峰里采样。
结果:安全左转(或右转)。
GMM 保证了这个点一定落在某个合理的峰值附近,为何是附近,而不是某个峰值 模拟手绘$x = \mu + \sigma \cdot \epsilon$ 模型通过预测 $\sigma$ 的大小,学会了什么时候该画得精准($\sigma$ 小),什么时候该画得潦草($\sigma$ 大);只要 $\sigma$ 不为 0,采样出来的点 $x$ 在数学概率上几乎不可能(概率为 0)正好等于 $\mu$,它只能是落在 $\mu$ 的附近。$\sigma$ 越大,落点离峰值就可能越远。
输出的si是什么? 一个笔画序列。
hi是怎么得到yi的? 通过一个全连接层投影得到yi
梯形里的softmax,GMM,simple是用来做什么的? softmax,处理3个笔触状态p和M个混合权重,确保二者各自总和为1。
维度相关,128,256,512 编码器中的参数z, µ , σ 都128维 过程h是256维度,最终h是512维度
编码器的s1->h1发生了什么?
训练时解码器是否参与?是否属于有条件生成? 参与,且属于有条件生成
训练时完整流程: 输入草图 → 编码器 → μ, σ → 重参数化 → z → 解码器 → 重建草图 ↓ 与原始草图比较计算损失 ↓ 反向传播更新所有参数什么是重建损失RL
# 重建损失 = 模型输出与原始输入的差异度量 原始草图 X → [编码器→解码器] → 重建草图 X̂ ↓ 计算差异 → 重建损失从输入到输出的全流程维度
输入草图序列 → 编码器处理 → h_final (512维) ↓ [分两个路径] ┌─────────────────────┐ ↓ ↓ W_μ (128×512) W_σ (128×512) ↓ ↓ μ (128维) logσ² (128维) ↓ ↓ └─────┬────────────────┘ ↓ ↓ μ (128) σ (128) ← exp(0.5*logσ²) ↓ ↓ 随机噪声ε ∼ N(0, I) (128) ↓ ↓ 重参数化采样 ↓ z = μ + σ ⊙ ε ↓ z (128维) ✓
混合高斯参数: (1, 123) # M=20 → 20*6 + 3 = 123 这是说yi么?
对于 M=20 个高斯分量,每个需要6个参数: 1. 均值 μ_x, μ_y (2个) - 位置 2. 标准差 σ_x, σ_y (2个) - 尺度 3. 相关系数 ρ (1个) - 形状(椭圆方向) 4. 混合权重 π (1个) - 该分量的权重 总共: 20 × 6 = 120个参数 3个logits,经过softmax得到概率: - q1: 笔落的logit - q2: 笔提的logit - q3: 结束的logit y_t = [高斯参数(120维), 笔状态logits(3维)] = 123维确定了高斯分量后是如何采样生成相对坐标的?
生成独立噪声: 从标准正态分布中抽取两个独立的随机数 $z_1$ 和 $z_2$。
计算 $\Delta x$: $\Delta x = \mu_x + \sigma_x \cdot z_1$
计算 $\Delta y$: 为了让 $y$ 与 $x$ 产生关联,我们需要利用相关系数 $\rho$: $\Delta y = \mu_y + \sigma_y \cdot (\rho \cdot z_1 + \sqrt{1 - \rho^2} \cdot z_2)$
采样后坐标与高斯分量的关系:每个高斯分量都代表局部不同的笔画走向 高斯分量是二维的,是一个椭圆云团
$\mu_x, \mu_y$ (均值向量):定义了分布的中心位置。
$\sigma_x, \sigma_y$ (标准差):定义了分布在 X 和 Y 方向上的伸展范围(缩放)。
$\rho$ (相关系数):定义了分布的旋转角度/关联度。
而采样得到的点就是云团中的一个坐标。
训练时:z来自编码器,$h_0$来自tanh处理,$c_0$呢?
状态 名称 作用 $h_0$ 隐藏状态 (Hidden State) 负责与当前的输入 $s_i$ 结合,直接决定当前步输出什么样的 GMM 参数(即决定“这一笔往哪画”)。 $c_0$ 细胞状态 (Cell State) 负责保存全局信息。随着画笔的移动,$c$ 会不断更新,确保模型记得画到了哪个阶段(比如画完了猫的头,该画耳朵了)。
怎么得到的?
$[ h_0 ; c_0 ] = tanh(W_zz + b_z)$ ,128维的z,做处理得到1024维,再分开为两个512维,一个是$h_0 $,一个是$c_0$
# 将隐向量 z 映射回解码器的初始隐藏状态 h0 和细胞状态 c0
self.fc_hc = nn.Linear(cfg.Nz, 2 * cfg.dec_hidden_size)
# 使用 z 初始化解码器的 h 和 c,并应用 tanh 限制数值范围
h, c = torch.split(torch.tanh(self.fc_hc(z)), self.cfg.dec_hidden_size, 1)
输入si得到yi+1,采样得到si+1,进行计算损失的么?这种损失是重构损失么?这种损失的计算是如何计算的?
重构损失 ($L_R$):衡量生成的笔画和原始笔画有多像。
KL 散度损失 ($L_{KL}$):衡量隐空间 $z$ 的分布是否符合标准正态分布
$L_R$的计算过程较为复杂:包含坐标损失(混合高斯负对数似然)、笔画损失。 坐标损失:$L_s = -\sum_{i} \log \left( \sum_{j=1}^{M} \pi_j \cdot \mathcal{N}((\Delta x, \Delta y)_{i+1} | \mu_j, \sigma_j, \rho_j) \right)$
传入真实相对坐标,$\mathcal{N}((\Delta x, \Delta y)_{i+1} | \mu_j, \sigma_j, \rho_j)) $这里是在说在指定高斯分量下,坐标落入云团的中心的概率,越远则值越小。 而坐标公式对M个高斯分量都这样计算,并且分别乘以对应的混合权重,再进行累加,log不改变概率,取反是为了实际代码的计算。
如果真实点正好落在模型预测的概率最高的“云团”中心,概率 $P$ 就大,$L_s$ 就小。训练过程就是不断把这些“云团”往真实点上拽。
笔划状态损失:交叉熵 (Cross-Entropy)
这部分比较简单,处理的是笔尖的动作(下笔、抬笔、结束)。
预测值:模型输出的 $p_{pen}$(3 维向量,如
[0.8, 0.1, 0.1])。目标值:真实的 One-hot 标签(如
[1, 0, 0])。计算: $L_p = -\sum_{i} \sum_{k=1}^{3} q_{i+1, k} \log(p_{i, k})$
- 这就是标准的分类损失,强迫模型在正确的时间学会“抬笔”或“收笔”。
具体解释就是累加3个状态下的损失,but,由于使用one-hot,3种状态中,真实标签那个为1,其余为0,故仅$-\log(p_{i, k})$ 当预测的笔触状态越大时,损失越小,否则越大(具体看下例)
| 变量 | 物理含义 | 维度/范围 | 详细解释 |
|---|---|---|---|
| $i$ | 时间步 (Time Step) | $0, 1, \dots, N$ | 代表当前画到了第几个点。 |
| $k$ | 状态类别 (Category) | $1, 2, 3$ | 代表三种动作:1-下笔绘制;2-抬笔移动;3-结束全画。 |
| $q_{i+1, k}$ | 真实标签 (Label) | $\{0, 1\}$ | 标准答案。第 $i+1$ 步时人类画家实际做的动作。通常是 One-hot 形式,如 [0, 1, 0]。 |
| $p_{i, k}$ | 预测概率 (Probability) | $[0, 1]$ | 模型预判。模型在第 $i$ 步预测“下一步($i+1$ 步)”发生动作 $k$ 的可能性。 |
场景设定
假设模型正在学习画一个圆。当前是第 $i=5$ 步,模型需要预测第 $6$ 步的动作。
真实情况($q_{i+1}$):第 6 步画家依然在纸上画线。所以真实状态是“下笔”,对应的 One-hot 标签为:
$$q_{i+1} = [1, 0, 0]$$即:$q_{6,1}=1$(下笔),$q_{6,2}=0$(抬笔),$q_{6,3}=0$(结束)。
模型预测($p_i$):模型在第 5 步结束时,输出层经过 Softmax 得到了三个概率值:
$$p_i = [0.7, 0.2, 0.1]$$即:模型有 70% 的信心认为下一步继续画,20% 认为要抬笔,10% 认为画完了。
第一步:套入求和公式
我们只看第 $i$ 步这一个点产生的损失:
$L_{p,i} = - \sum_{k=1}^{3} q_{i+1, k} \log(p_{i, k})$
将 $k=1, 2, 3$ 的值全部代入:
$L_{p,i} = - [ (q_{6,1} \cdot \log p_{5,1}) + (q_{6,2} \cdot \log p_{5,2}) + (q_{6,3} \cdot \log p_{5,3}) ]$
第二步:代入具体数值
$L_{p,i} = - [ (1 \cdot \log 0.7) + (0 \cdot \log 0.2) + (0 \cdot \log 0.1) ]$
因为真实标签中只有正确项($k=1$)是 $1$,其余都是 $0$,所以后两项直接消失了。计算简化为:
$L_{p,i} = - \log(0.7)$
第三步:计算最终 Loss 值
查对数表或计算器:$\log(0.7) \approx -0.356$
$L_{p,i} = - (-0.356) = \mathbf{0.356}$
对比分析:如果模型猜错了会怎样?
情况 A:预测非常准
如果模型预测 $p_i = [0.95, 0.04, 0.01]$(信心极强):
$Loss = -\log(0.95) \approx \mathbf{0.051}$
结论:Loss 很小,参数调整幅度会很小。
情况 B:预测严重错误
如果模型预测 $p_i = [0.1, 0.8, 0.1]$(模型误以为要抬笔了):
$Loss = -\log(0.1) \approx \mathbf{2.302}$
结论:Loss 变大了 45 倍!模型会受到巨大的“惩罚”,从而在反向传播中大幅度修改权重。
代码实战——理论与实践的偏差
数据3维
问题:实际训练的数据集是3维的,文章中是5维的,我们需要预处理为5维的进行训练。 这里原始数据的状态用1个bit表示,0为画线中,1为抬起。
解答:准备一个空的5维,平移原始数据的前2维,若原始数据第3维为0,则新数据的第3维为1(表示笔尖触碰纸),若原始数据第3维为1,则新数据的第4维为1(表示抬笔)。对于新数据第5维的处理,我们默认一幅画的前n-1条数据的第5维都是0,仅在第n条数据(最后一条数据)上将第5维置为1