稳定性:雷同元素在排序后前后相对位置不变;
稳定排序口诀:冒插归基计(注意:插入排序中希尔排序不稳定)
希尔排序:
特点/排序过程:指定“步长“,分组执行插入排序,缩小“步长”,分组执行插入排序,直到步长为0(此时每个分组中仅含1个元素),此时序列基本有序,再对序列整体进行最后一轮插入排序。
由上特点可见(插入排序共有的特点):
- 序列有序有利于插入排序(包含希尔排序)
- 每轮排序无法确定一个元素的最终位置
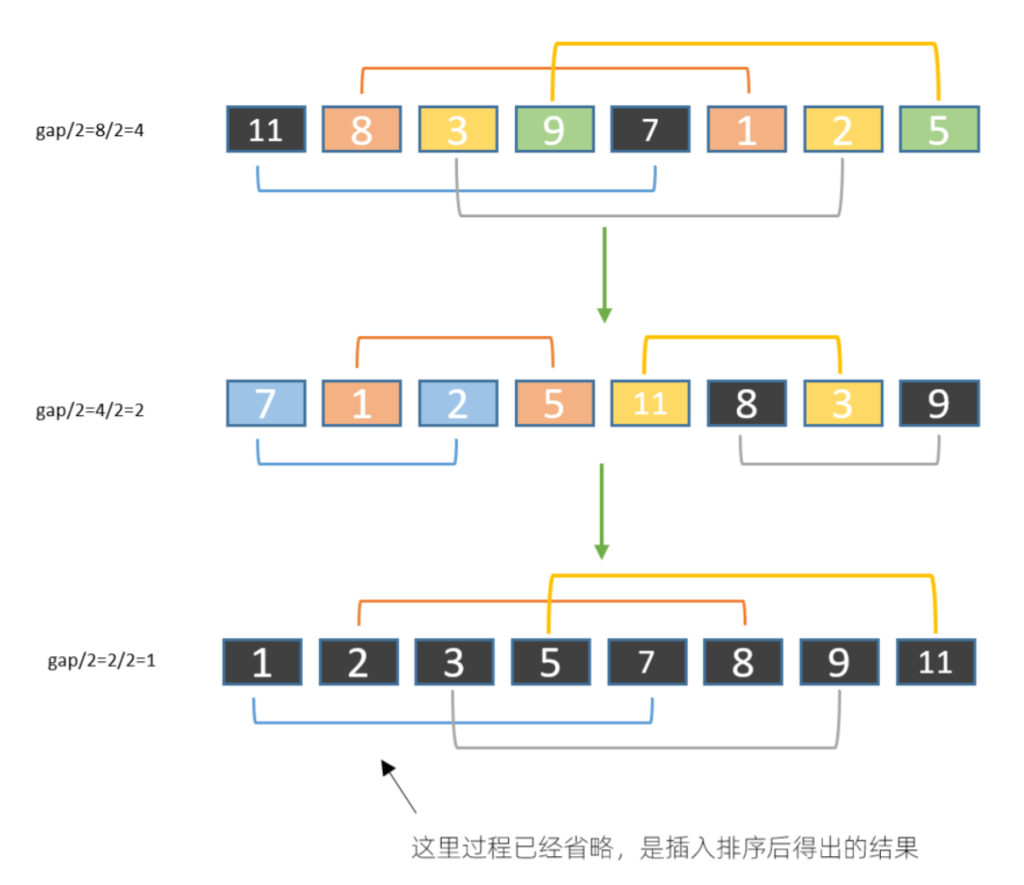
注意⚠️计算“步长”时自身并不计入步长,而是从自己开始往后数“步长”个数。
简单插入排序
特点/排序过程:默认第一个元素有序,其左边为有序一方,右边无序;每轮排序将无序一方的第一个元素同有序一方的每个元素依次比较(从左方的最后面开始比较),直到找到合适的位置进行插入(每轮仅进行一次插入)
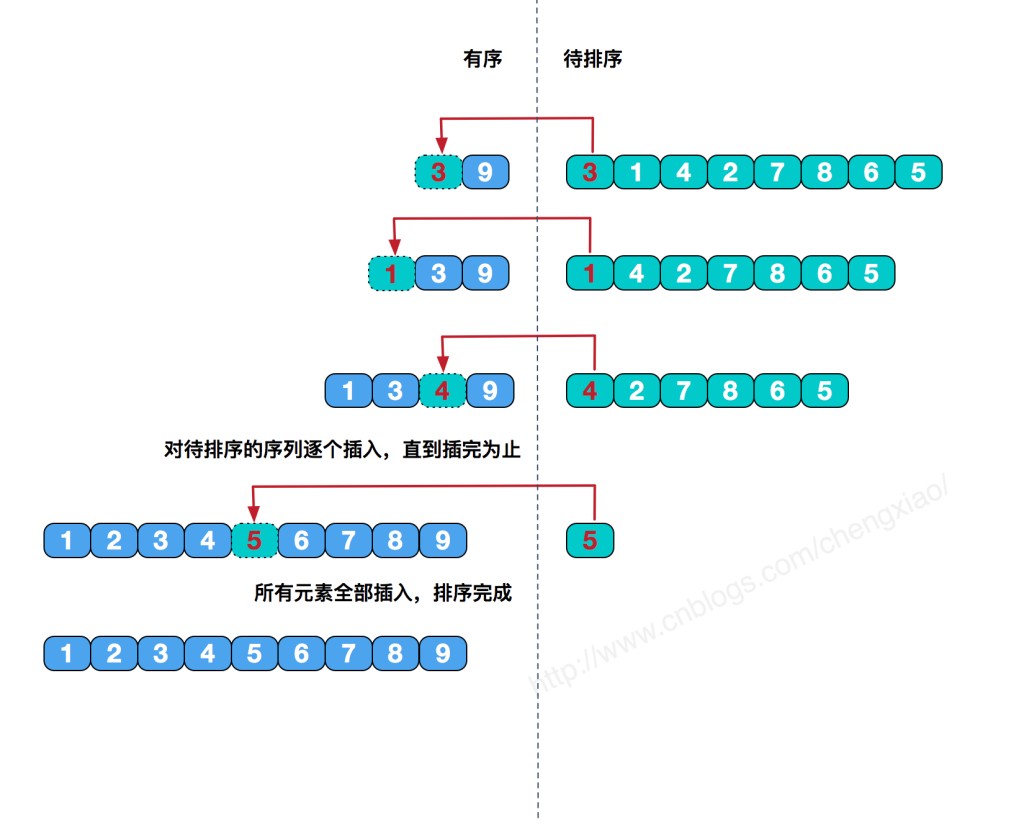
折半插入排序
鉴于,插入排序序列的左部分是有序的,故在为右方无序元素查找合适位置时,可以使用二分查找,减少比较次数。
冒泡排序
假设升序排序,从左边开始比较第一个元素和第二个元素大小,如第一个更大则交换二者位置,交换之后再去比较第二个和第3个…这样比较直到第n-1个和第n个相比较,此时一轮比较结束,末尾元素为序列中最大的一个。
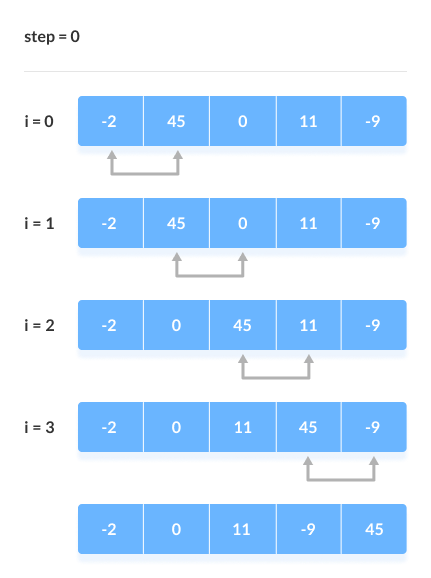
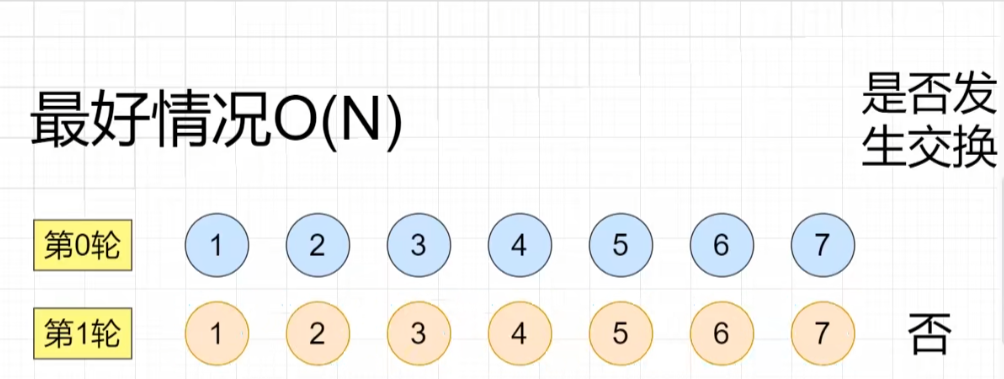
注意⚠️:如排序中任一轮次未发生交换则序列有序,排序结束。
快速排序
每轮排序,找“基准”,大于基准值的都放右边,小于基准值的都放左边,这样就形成了左右两个子序列;再分别对左右两个子序列进行此类找基准,放左右的操作,一直这样,分放分放,直到每个子序列中仅包含一个元素。
- Worst Case Complexity [Big-O]:
O(n<sup>2</sup>)
It occurs when the pivot element picked is either the greatest or the smallest element.
This condition leads to the case in which the pivot element lies in an extreme end of the sorted array. One sub-array is always empty and another sub-array containsn - 1elements. Thus, quicksort is called only on this sub-array.
However, the quicksort algorithm has better performance for scattered pivots.- Best Case Complexity [Big-omega]:
O(n*log n)
It occurs when the pivot element is always the middle element or near to the middle element.
最佳:每次划分的两个子序列中元素数量不相上下
最差:一个子序列包含n-1个元素,一个子序列无元素
由上特点可见:
- 序列有序无益于快速排序,but有序有利于冒泡排序
- 每轮排序可以确定至少一个元素的最终位置(冒泡确定一个,快排确定>=1个)
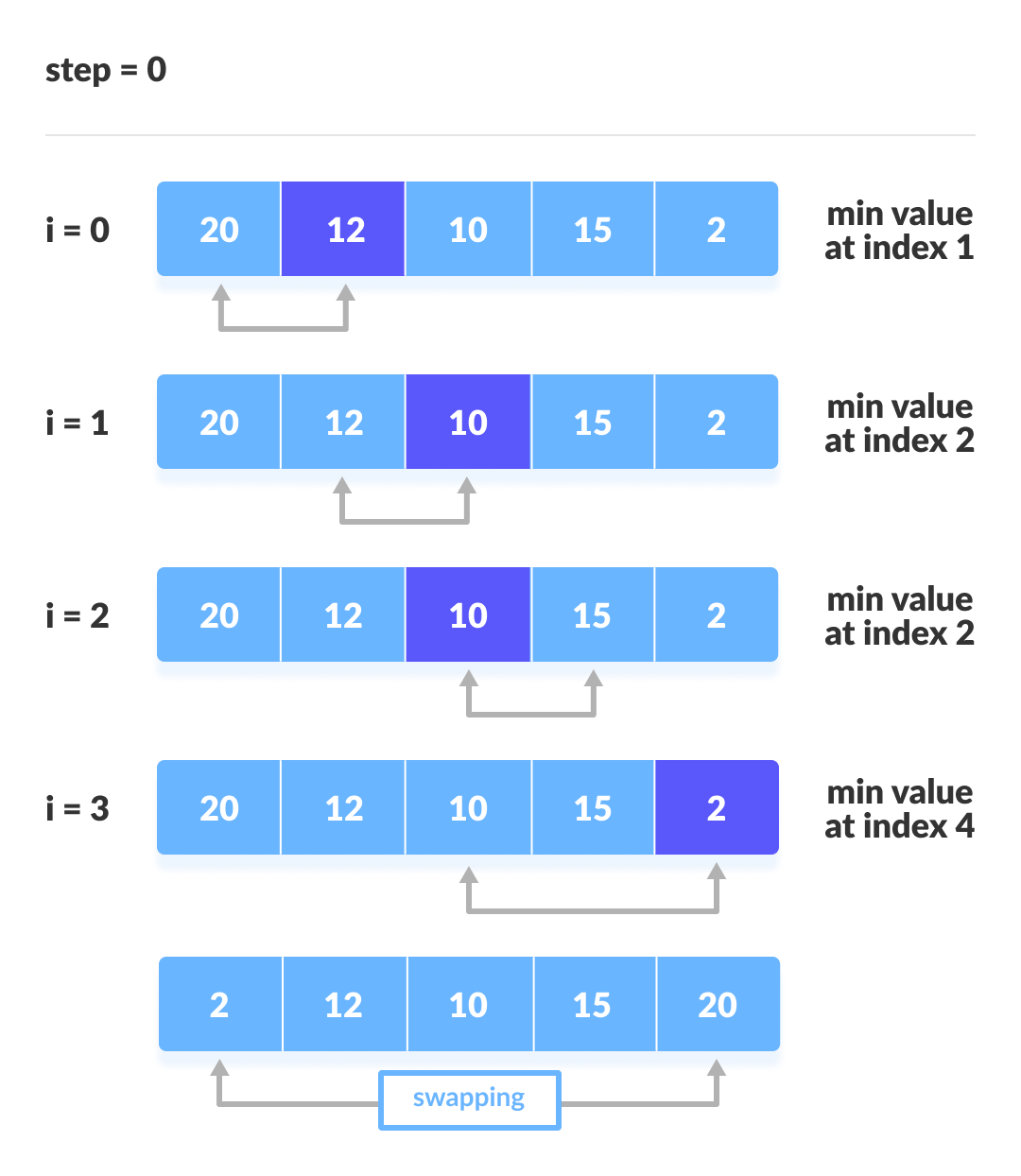
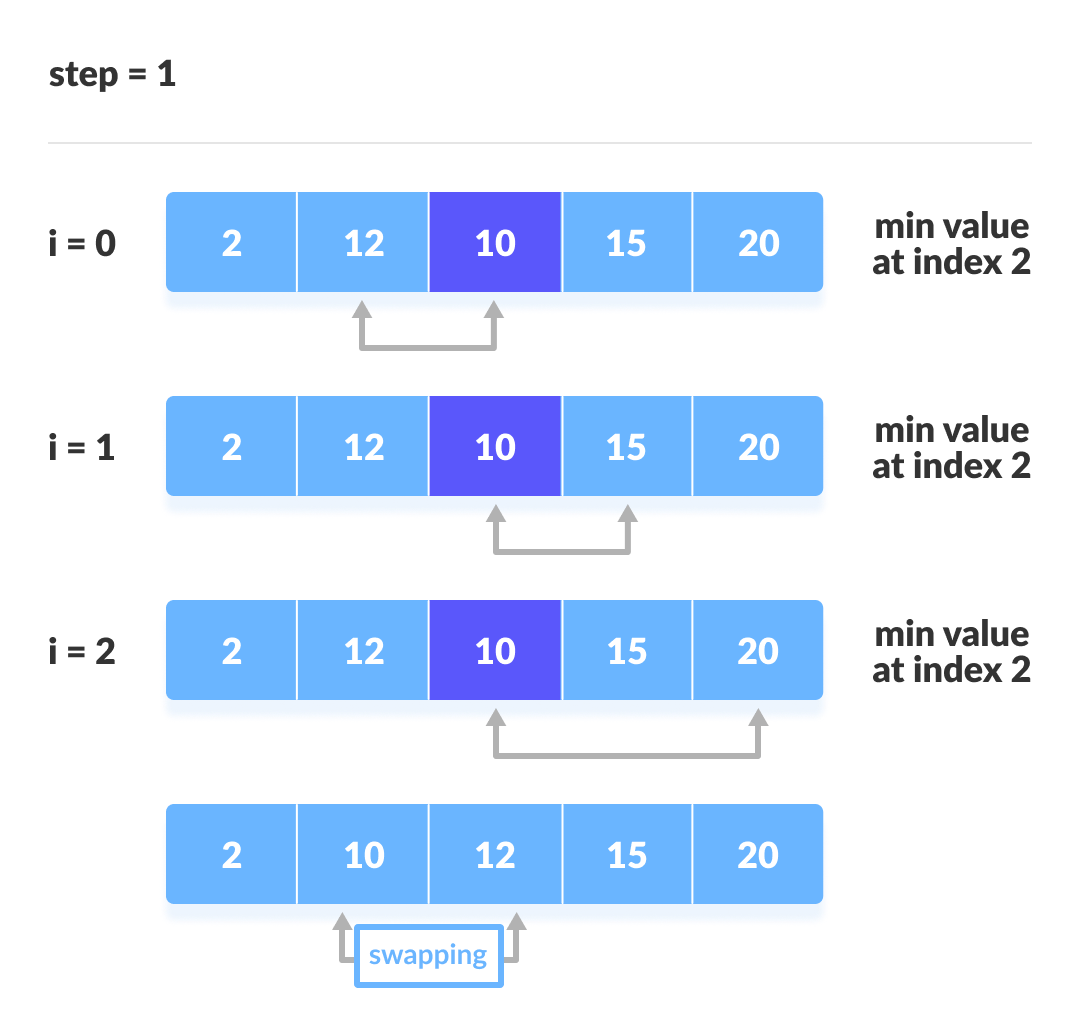
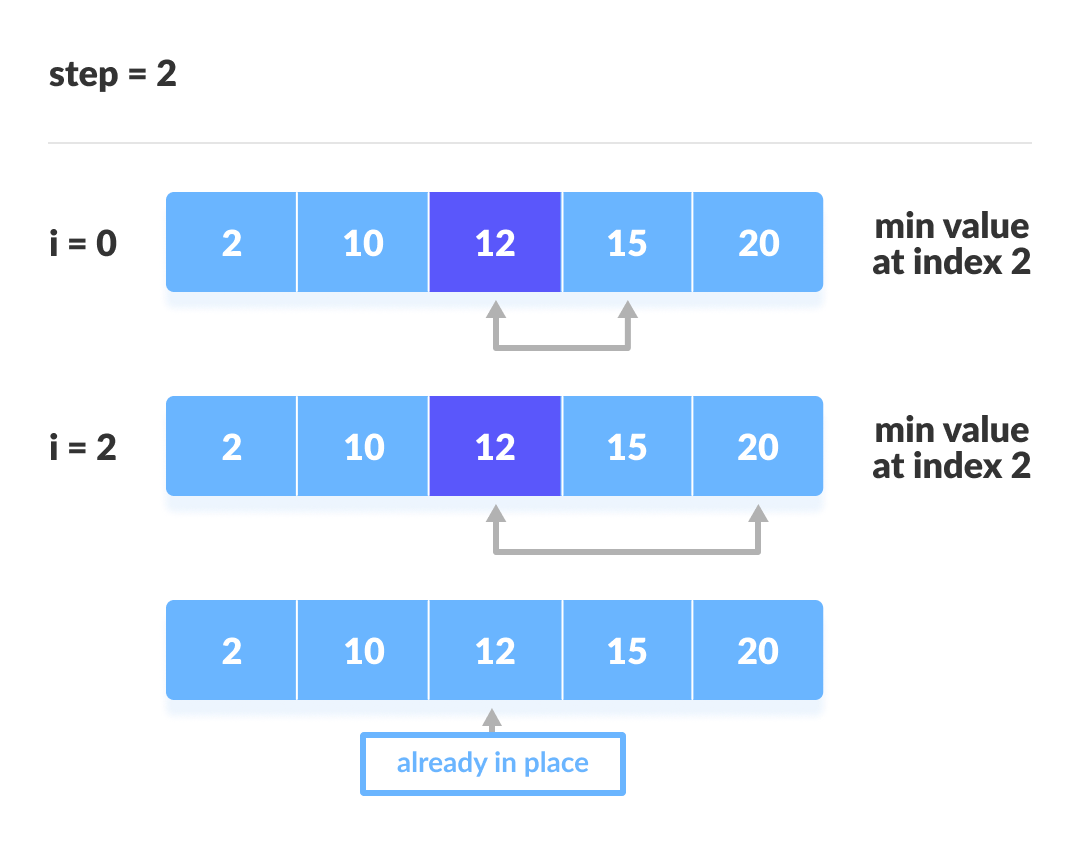
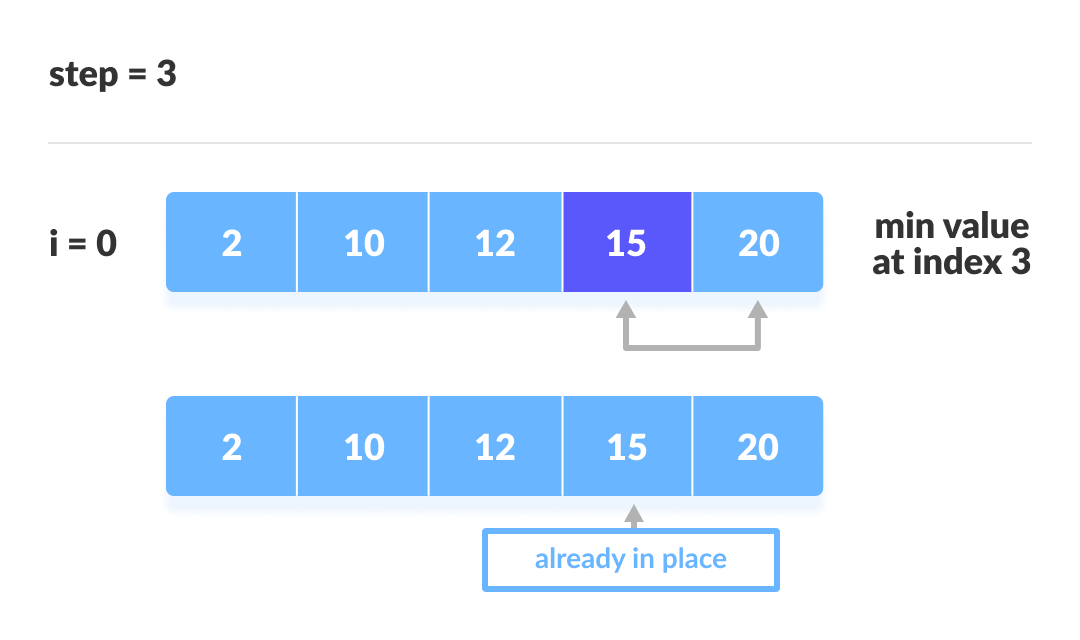
简单选择排序
每轮选择一个最小的数放置于无序序列的最前方,有序序列的最后方。
特点:O(n^2)恒定,且序列有序无序均不影响简单选择排序的执行效率。
基数排序
假设10进制情况,则选定0~9,从个位开始,将序列进行扫描,是几就放到0~9中几的下面,(如8,则放到8的下面)。一轮结束从0开始依次取出元素,再对十位进行此类排序…直到排序完成。

特点:不受序列有序无序影响,排序稳定。
计数排序
创建一个数组,该数组大小为序列中最大值的大小,将该数组元素初始化为0;
对序列进行遍历,记录每一个数值出现的频率(数组用来做key value映射,index作为序列中的值,value用于记录频率),最后根据这个频率即可得到有序序列。



